描述
假设网络中有N个节点，以相同的概率p随机连接网络中的一对节点。ER随机图模型的平均度<1>=P（N-1）≈PN[1]中给出在N→∞时的度分布函数
，说明ER随机图的度分布是围绕<k>的泊松分布。
由于在随机图模型中任意两点间连边的概率为p，即任意一个节点的邻点之间的连边概率也为p，因此随机图模型的平均集聚系数
。考虑到ER随机图的构造方式，任选一个节点，与其距离为1的节点数为<k>，且节点之间相连的概率是一致的，因此与其距离为2的节点数为<k>2，由此类推，网络中与任意节点距离为l的节点数为<k>l。由于度分布为泊松分布，因此可认为所有节点对之间的距离近似于网络的平均路径长度<l>，即与任意节点距离为<l>的节点数为N，记作
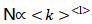，可得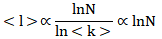
。
ER随机图的统计特性显示，平均度与节点数N成正比，度分布遵循泊松分布；其平均路径长度与lnN成正比，说明即便是规模很大的ER随机图也可能拥有很小的路径长度，和规则网络显然不同，反映了随机图的小世界特性；网络中平均集聚系数与N成反比，说明大规模的ER模型里节点没有集聚的现象，结构上比一般具有明显集聚现象的真实复杂网络更随机。
参考文献
[1] Erdős P, Rényi A. On the strength of connectedness of a random graph[J]. Acta Mathematica Hungarica, 1961, 12(1-2): 261-267.
