定义
非线性效应和色散效应处于某种特定的平衡的脉冲。
通常情况下,当脉冲在透明介质中传播时,由于克尔效应和色散作用会导致脉冲的时域和频域形状的变化。但是在某种特定的情况下,除了随传播距离变化而产生的相位延迟外,克尔非线性效应和色散效应对于脉冲的作用会相互抵消,因此脉冲的时域和频域形状在很长的传播距离内都不会发生变化[1,3]。这个现象是在水波中首先被发现的,但是后来在光纤中也发现了该现象。 无损耗介质中(基阶)孤子的传播条件为:
1、对于正的非线性系数n2(大多数介质的非线性系数都是正的),其色散必须为反常色散;
2、脉冲的时域形状需要为无啁啾的双曲正割形(假设群延迟色散为常数,也就是说没有高阶色散):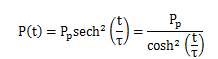
3、脉冲能量Ep和脉宽τ满足以下条件: 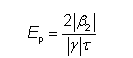
其中γ是非线性系数,单位为rad/(Wm);β_2是群速度色散(即单位长度的群延迟色散)。需要注意的是脉宽τ不是脉冲的时域半高全宽(FWHM),脉冲的时域半高全宽(FWHM)=1.7627×τ。
当满足以上条件时,脉冲可以以孤子的形式(即时域和频域形状保持不变)传输。其在一定的传输距离下只会经历一个大小固定的相移,该相移的大小为脉冲峰值所经历的由非线性效应导致的相位延迟的一半(如图1所示)。孤子的相移在时域和频域上都是恒定的,因此其不会导致啁啾或者频域展宽。
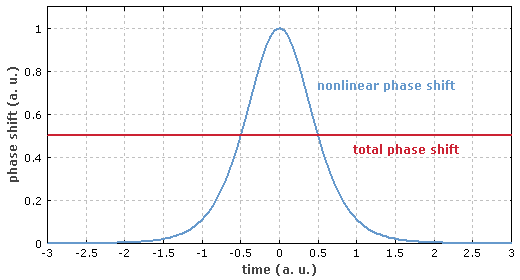
图 1 蓝色曲线:时域上的非线性相移(无色散作用),其正比于光强;红色曲线:脉冲经历的由非线性作用和色散作用导致的整体相移,这样一个不随时间变化的相移不会导致脉冲的时域或者频域的形状变化
一个例子:标准通信光纤中的孤子
以下给出了在标准通信光纤(1.5um区域的单模光纤)中的孤子。以康宁的SMF-28e光纤为例,其在1550nm处的有效模场面积为85 μm2,因此其非线性系数为1.43mrad/(Wm)。(石英的非线性折射率系数取为3 × 10−16 cm2/W)。该光纤在1550nm处的色散为16.2ps/(nm km),即−20 660 fs2/m。利用上述方程,我们得到1ps的孤子的能量为51pJ,其峰值功率为45W。 如果是脉宽为100fs(原先的1/10)的飞秒光,其脉冲能量则变为510pJ(原先的10倍),而峰值功率变为4.5kW(原先的100倍)。
孤子的稳定性
其实孤子最为显著的特征并不是上面所说的色散和非线性之间的平衡,而是最为非线性波动方程的孤子解都非常稳定:即使初始脉冲距离精确的孤子解具有一定的偏差,脉冲也会自动的“找到”正确的孤子形状,将一部分能量剥离出变为所谓的色散波。色散波为一种很弱的背景,几乎不会造成什么非线性效应,并且由于色散的影响会在时域上分散开来。即便有一定的介质性质的变化,孤子也很稳定,条件是这些变化在传播距离与所谓的孤子周期(定义为恒定相位延迟为π/4的传播距离)相比更长的情况下发生。这意味着,孤子可以绝热的调整其形状以适应缓慢变化的介质参数。另外,孤子可以容纳于一定的较高阶色散,自动调整为给定色散条件下的满足上述的平衡的特殊形状。
高阶孤子
如果脉冲能量是基阶孤子能量的整数平方倍,脉冲则为所谓的高阶孤子。这样的脉冲不能保持其形状的,而是周期性地变化,其周期即为上述的孤子周期。
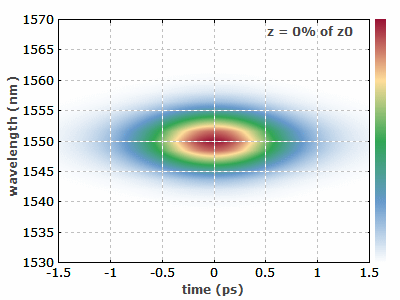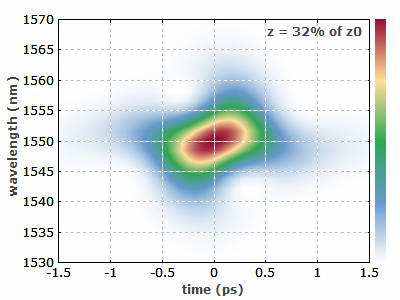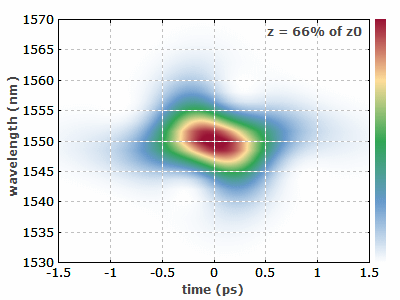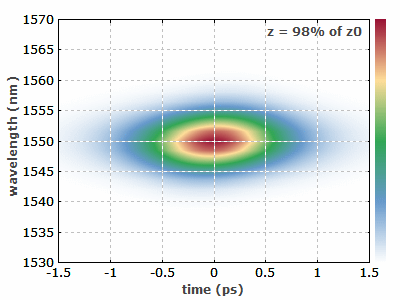
图 2 此动图显示了一个三阶孤子如何在光纤中演变的过程。较高阶的孤子具有更复杂的过程。
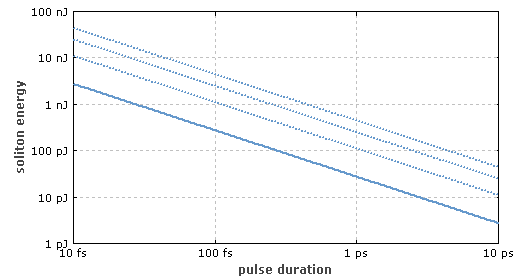
图 3 单模光纤中孤子脉冲能量和脉冲脉宽之间的关系。实线为基阶孤子,虚线为高阶孤子(阶数分别为2,3,4)。 受到高阶色散和其它效应的干扰,高阶孤子会分裂为基阶孤子。因此高阶孤子远没有基阶孤子那么稳定。
孤子的重要性
基阶孤子脉冲是非常重要的,特别是对于长距离光纤通信和锁模激光器而言。在后一种情况下,当腔内的总的色散和非线性很弱时会形成类孤子脉冲。孤子还在各种技术利用光纤进行脉冲压缩,如绝热孤子压缩和高阶孤子压缩。
孤子自频移
当在光纤中传播,孤子不仅仅受到克尔效应的作用,还有受激拉曼散射的作用。对于非常短的孤子(如脉宽<100飞秒时),光谱变得很宽,因此波长较长的部分可以通过消耗更短波长的光作为泵浦来获得放大。这使得孤子朝较长的波长移动,这也就是所谓的孤子自频移[5,6,12,16,17]。这种效应的强度在很大程度上取决于脉冲的持续时间,因为更短的孤子表现出更高的峰值功率和更宽的光谱。其中后者更为重要,因为拉曼增益在小频率偏移时很小。在传播过程中,所述的频移速率往往会越来越慢,因为在脉冲能量变低了而且脉冲宽度也增加了[17]。 利用孤子自频移可以使得孤子进入原来难以达到的光谱区域。通过在调整光纤中的脉冲能量,可以在一个大的范围内获得可调节的波长输出[10,11,13-15]。
耗散孤子
以上讨论中脉冲不与光纤进行能量交换。因此,这些孤子被称为保守孤子(conservative solitons)。但是更常见的情况下耗散效应会起作用。例如,即便光纤具有正常色散和正的非线性折射率系数,也可能出现所谓的耗散孤子,这种情况下有额外的光谱带通滤波效应和光学增益(放大)以补偿在滤波器中的能量损耗。另一种可能的耗散作用是饱和吸收。 虽然很难想象有这样一个光纤使得以上的所有这些效应都存在,从而形成一个耗散孤子。但是人们可以通过包含有光纤,滤波器和可饱和吸收体的锁模激光器的谐振腔来实现以上过程。如果以上每个效应在谐振腔的一个循环中都足够弱,那么这与将这些效应平均分布在光纤中所得到的动力学过程是十分接近的。在这种情况下,在这些锁模光纤激光器中运转的脉冲就被称为耗散孤子。 需要注意的是,严格来说在锁模激光器,我们永远不可能得到所谓的保守孤子,因为锁模激光器中总是有一些饱和吸收体和增益存在。这导致的结果是脉冲能量和脉冲持续时间会处于一个稳定态:在这种状态下,光纤中孤子的能量和脉宽会在一个大的范围内变化,但是其乘积是固定的。这些固定的参数其实就是色散孤子的特征。然而,由于这种情况下的脉冲整形效果往往是保守的(即只有色散和非线性),我们并不称这些脉冲为耗散孤子。
空间孤子
除了如以上所讨论的时间孤子,还存在一种所谓的空间孤子。在这种情况下,介质(很可能是光折射型的)的非线性可以抵消衍射,使得光束以恒定的光束半径在这种原本为各向同性的介质中传播。
参考文献
[1] J. S. Russell, “Report on waves”, in Report of the 14th meeting of the British Association for the Advancement of Science, p. 331 (1844)
[2] V. E. Zakharov and A. B. Shabat, “Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media”, Sov. Phys. JETP 34, 62 (1972)
[3] A. Hasegawa and F. Tappert, “Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion”, Appl. Phys. Lett. 23, 142 (1973)
[4] L. F. Mollenauer, R. H. Stolen, and J. P. Gordon, “Experimental observation of picosecond pulse narrowing and solitons in optical fibers”, Phys. Rev. Lett. 45 (13), 1095 (1980)
[5] F. M. Mitschke and L. F. Mollenauer, “Discovery of the soliton self-frequency shift”, Opt. Lett. 11 (10), 659 (1986)
[6] J. P. Gordon, “Theory of the soliton self-frequency shift”, Opt. Lett. 11 (10), 662 (1986)
[7] L. F. Mollenauer et al., “Soliton propagation in long fibers with periodically compensated loss”, IEEE J. Quantum Electron. QE-22, 157 (1986)
[8] N. N. Akhmediev et al., “Stable soliton pairs in optical transmission lines and fiber lasers”, J. Opt. Soc. Am. B 15 (2), 515 (1998)
[9] V. N. Serkin and A. Hasegawa, “Novel soliton solutions of the nonlinear Schrödinger equation model”, Phys. Rev. Lett. 85 (21), 4502 (2000)
[10] X. Liu et al., “Soliton self-frequency shift in a short tapered air–silica microstructure fiber”, Opt. Lett. 26 (6), 358 (2001)
[11] N. Nishizawa and T. Goto, “Widely wavelength-tunable ultrashort pulse generation using polarization maintaining optical fibers”, IEEE J. Sel. Top. Quantum Electron. 7 (4), 518 (2001)
[12] J. Santhanam and G. P. Agrawal, “Raman-induced spectral shifts in optical fibers: general theory based on the moment method”, Opt. Commun. 222, 413 (2003)
[13] K. S. Abedin and F. Kubota, “Widely tunable femtosecond soliton pulse generation at a 10-GHz repetition rate by use of the soliton self-frequency shift in photonic crystal fiber”, Opt. Lett. 28 (19), 1760 (2003)
[14] E. R. Andresen et al., “Tunable light source for coherent anti-Stokes Raman scattering microspectroscopy based on the soliton self-frequency shift”, Opt. Lett. 31 (9), 1328 (2006)
[15] M.-C. Chan et al., “1.2- to 2.2-μm tunable Raman soliton source based on a Cr:forsterite laser and a photonic-crystal fiber”, IEEE Photon. Technol. Lett. 20 (11), 900 (2008)
[16] J. H. Lee et al., “Soliton self-frequency shift: experimental demonstrations and applications”, IEEE J. Quantum Electron. 14 (3), 713 (2008)
[17] A. A. Voronin and A. M. Zheltikov, “Soliton self-frequency shift decelerated by self-steepening”, Opt. Lett. 33 (15), 1723 (2008)
[18] P. Grelu and N. Akhmediev, “Dissipative solitons for mode-locked lasers”, Nature Photon. 6, 84 (2012)
[19] R. Paschotta, case study on higher-order solitons
参阅:克尔效应、色散、孤子周期、双曲正割型脉冲、高阶孤子、绝热孤子压缩、脉冲压缩



