定义
光学谐振器(或谐振光学腔)是光学元件的排列,它允许光束在封闭路径中循环。 这种谐振器可以以非常不同的形式制造。
带大块元件的谐振器与波导谐振器的比较
光学谐振器可以由块状光学元件制成,如图1所示,也可以由波导谐振器制成,其中光被引导而不是通过自由空间发送。
例如,体光学谐振器用于固态体激光器。 它们的横向模式特性取决于整体设置(包括气隙的长度),并且模态大小可能会沿谐振器发生显著变化。 在某些情况下,模式属性也会受到热透镜效应等效应的显著影响。
波导谐振器通常由光纤(例如光纤激光器)或集成光学器件的形式制成。 横向模式属性(见下文)由波导的局部属性决定。
还有混合类型的谐振器,包含波导和具有自由空间光传播的部分。 例如,这种谐振器用于某些光纤激光器,其中需要将体光学元件插入激光谐振器中。
线性谐振器与环形谐振器
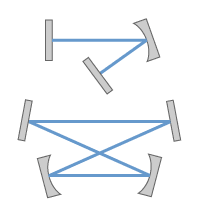
图1:一个简单的线性光学谐振器,带有一个弯曲的折叠镜(顶部)和一个四镜领结环谐振器(底部)。
线性(或驻波)谐振器(图1,顶部)的制造使得光线在两个端镜之间来回反射。 对于连续循环的光,总是存在反向传播波,它们相互干扰形成驻波模式。
在环形谐振器中(图1,底部),光可以在两个不同的方向上循环(另见:环形激光器)。 环形谐振器没有端镜。
在任何一种情况下,谐振器都可能包含在每次往返中通过的附加光学元件。 例如,激光谐振器包含一个增益介质,可以补偿光的每次往返中的谐振器损耗。
在谐振器往返过程中,光会经历各种物理效应,从而改变其空间分布:光学元件的衍射、聚焦或散焦效应(有时涉及光学非线性),在特殊情况下也会获得引导、可饱和吸收等。
线性谐振器和环形谐振器之间的一些重要区别是:
- 在环形谐振器中,光可以在两个不同的方向上循环。 如果有一个输出耦合器镜,则会导致两个不同的输出波束。 末端带有输出耦合器的线性谐振器不会出现这种现象。
- 在环形激光器的情况下,谐振器内的光学元件每往返一次被光击中一次,在线性谐振器中每往返两次(端镜除外)。
- 当光通过部分透明的镜子注入线性谐振器时,反射光可以传播回光源。 环形谐振器的情况并非如此。 因此,环形谐振器有时优选用于对光反馈敏感的激光源的谐振倍频。
- 线性体谐振器可以有两个稳定区(见下文),例如内部透镜的屈光度功率或谐振器臂长度的变化。 环形谐振器只有一个稳定区。 (如果内部透镜在环形谐振器中每次往返通过一次以上,或在线性谐振器中通过两次以上,则可能存在更多的稳定区。
- 如果环形谐振器反射镜具有曲面,则光在环形谐振器的每个谐振镜上的非正常入射会导致散光。 蝴蝶结环谐振器几何形状通常用于通过保持较小的入射角来最大程度地减少散光。
- 具有高Q因数的单片环形谐振器可以利用所有表面的全内反射,因此可能不需要任何介电镜。
稳定与不稳定的体光学谐振器
体光学谐振器的稳定性本质上意味着注入系统的任何具有初始横向偏移位置和角度的光线都将在许多往返行程中停留在系统内。 对于不稳定的谐振器,有些射线的横向偏移会无限增加,因此它们将离开光学系统。
谐振器的稳定性取决于光学元件的特性和排列,基本上取决于反射面的曲率、其他聚焦效应以及元件之间的距离。 当臂长或谐振器中聚焦元件的屈光度功率等参数发生变化时,谐振器可能会经过一个(对于环形谐振器)或两个(对于驻波谐振器)稳定区[2]。 在这种稳定区的边缘,谐振器末端的波束尺寸可能发散或趋于零,对准灵敏度也可能发散。
大多数固态体激光器基于稳定的谐振器,但不稳定谐振器在某些激光器中具有优势,特别是那些具有非常高输出功率和高激光增益的激光器,可以实现更好的光束质量。 不稳定谐振器的模式具有相当复杂的特性。 输出耦合通常使用高反射镜完成,其中部分循环光在边缘周围(或可能仅在一侧)丢失。 另一种可能性是使用具有横向反射率变化的部分透射输出耦合器镜(高斯反射率镜)。
谐振器模式
谐振器模式本质上是光的自洽场分布 - 更准确地说,在每次谐振器往返中自我再现(除了可能的功率损失)的电场分布。
谐振器模式的属性在很大程度上取决于各种细节:
- 在波导谐振器中,横向模态结构仅由波导属性决定,如果波导属性恒定,则谐振器中的任何地方都是恒定的。 只能存在单个横向振型,例如,如果使用单模光纤。
- 在体光学谐振器中,模式属性取决于整体光学设置,并且在稳定谐振器和不稳定谐振器之间差异很大(见上文)。 对于稳定的谐振器,可以描述横向模式模式,例如使用Hermite-Gaussian函数。 最低阶模式(轴向模式、基波模式)具有最简单的轮廓;更复杂的形状对应于高阶模式。 模式属性可以使用ABCD 矩阵算法进行计算。 不稳定谐振器表现出更复杂的模式结构,只能用数值平均值计算。 通常,横向模径沿谐振器轴线变化。
对于每个横向模式模式,只有某些光学频率在每次往返后自一致地再现光学相位(即往返相移是2π的整数倍)。 这些被称为模频率或共振频率,并且大致等距(但由于色散,不完全等距)。 谐振器模式的频率间隔,也称为自由频谱范围(FSR),是反向往返时间,或者更准确地说是反向往返群延迟。 这意味着随着谐振器长度的增加,FSR会变小。 频率间隔与谐振宽度(谐振器带宽)的比值称为精细度,由谐振器每次往返的功率损耗决定。 一个相关的度量是Q因子,它是谐振频率和带宽的比值。
关于谐振器模式的文章提供了更多详细信息。
共振增强
例如,如果端镜部分透明,则可以将光从外部送入谐振器。 当(单色)输入光的频率与其中一个模态的频率匹配,并且空间形状也匹配(→模匹配)时,可以实现最高的内部光功率(以及通过谐振器的最大透射率)。 特别是对于低损耗谐振器,通过谐振增强(→增强腔),循环腔内功率可以大大超过输入功率。
当脉冲序列的频率与光学共振相匹配时,常规光脉冲序列也可以进行共振增强。 在时域中,这意味着脉冲周期与谐振器的往返时间相匹配,或者与其整数部分相匹配。
体光学谐振器的微妙特性
体光学谐振器的物理学在自然界中令人惊讶地丰富。 一些有趣的方面是:
- 具有横向光学增益或损耗变化的谐振器的模式通常不形成正交函数集。 这些非正常模式具有一些特殊的属性。 例如,这些模式叠加的总功率不仅仅是不同模式下功率的总和。 在某些情况下,非正态模式的谐振器可以用复杂的高斯光束分析来处理,其中ABCD矩阵的元素和高斯光束半径可以是复数。
- 在一般散光的情况下(例如在一些非平面环形激光谐振器中),存在有趣的效果,例如图像旋转,偏振旋转和所谓的扭曲光束。
- 有一些技术上有趣的方法(通常是数值性质的)来设计具有给定属性的谐振器。
- 激光谐振器的设计对激光操作的各个方面都有重要影响,例如对准灵敏度和光束质量。
微谐振器
有各种形式的非常小的谐振器微谐振器,即尺寸只有几微米甚至更小。 可用技术的一些示例:
- 带有布拉格反射镜的极短驻波谐振器通常用于半导体光电子学,例如分布式反馈激光器和垂直腔面发射激光器。
- 相当小的环形谐振器可以用光子集成电路上的波导实现,例如用绝缘体上的硅技术实现。 即使是更小的谐振器也可以以光子晶体的晶格缺陷的形式实现。
- 有环形微谐振器,一种环形谐振器,光可以与锥形光纤耦合。
- 人们可以在微小的透明球体中使用耳语画廊模式,再次将光与锥形光纤耦合。
尺寸非常小的光学谐振腔具有较大的自由光谱范围,这对于应用通常非常重要。
光学谐振器的应用
光学谐振腔用于以下目的:
- 作为激光谐振器,其中谐振器损耗由增益介质补偿,以维持或建立光功率
- 作为过滤光辐射频率含量的标准具
- 用于过滤光辐射的横向形状(→型清洁腔)
- 作为短期光学频率标准(例如,当激光的频率锁定在稳定参考腔的共振频率时))
- 用于精确的长度测量,例如,利用谐振器长度变化时周期性发生的共振
- 用于利用腔内功率的共振增强(→增强腔),例如为了实现来自低功率单频激光器的光的高效倍频
- 用于通过记录腔内辐射功率衰减(腔衰荡光谱)来精确测量低水平损耗)
- 用于产生色散效应,例如使用Gires-Tournois干涉仪
参考文献
[1] L. W. Casperson, “Mode stability of lasers and periodic optical systems”, IEEE J. Quantum Electron. 10 (9), 629 (1974), doi:10.1109/JQE.1974.1068485
[2] V. Magni, “Multielement stable resonators containing a variable lens”, J. Opt. Soc. Am. A 4 (10), 1962 (1987), doi:10.1364/JOSAA.4.001962
[3] M. Notomi et al., “Optical bistable switching action of Si high-Q photonic-crystal nanocavities”, Opt. Express 13 (7), 2678 (2005), doi:10.1364/OPEX.13.002678
[4] J. Bravo-Abad et al., “Enhanced nonlinear optics in photonic-crystal microcavities”, Opt. Express 15 (24), 16161 (2007), doi:10.1364/OE.15.016161
[5] P. Lalanne et al., “Photon confinement in photonic crystal nanocavities”, Laser & Photon. Rev. 2 (6), 514 (2008), doi:10.1002/lpor.200810018
[6] A. E. Siegman, Lasers, University Science Books, Mill Valley, CA (1986)
[7] N. Hodgson and H. Weber, Laser Resonators and Beam Propagation, 2nd edn., Springer, Berlin (2005)
[8] Blog article: “The resonator mystery”



