定义
应用于激光增益介质的吸收和发射特性的理论,特别是固态介质。
特别是在固态激光器的背景下,人们经常处理斯塔克能级流形,其中简并由晶体场的影响解除。 因此,斯塔克流形之间的吸收和发射跃迁具有显著的光谱宽度(带宽)。 波长相关的跃迁强度用有效跃迁截面描述。
在1960年代,贝尔实验室的Dean E. McCumber制定了一个详细的理论[1] - 现在称为McCumber理论 - 以探索激光增益介质(如分子气体)的各种光学特性之间的定量关系,以及稀土掺杂或过渡金属掺杂的激光增益介质。 他利用热力学原理,遵循阿尔伯特·爱因斯坦早期(和不太一般的)理论研究。
McCumber理论对于准三能级激光增益介质(例如稀土掺杂型)的光谱评估特别有用。 一个至关重要的结果是麦坎伯关系(或麦坎伯方程)
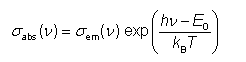
与频率相关的有效转换截面相关σ腹肌用于吸收和σem用于相互排放。 数量E0,它取决于温度而不是光学频率ν,可以从单个斯塔克能级的能量计算出来,如果这些能量是已知的。 否则,人们可以根据每个斯塔克能级流形内的能级能量等距的假设得到估计[3]。 或者E0可以使用互易法或富希特鲍尔-拉登堡方程等进行校准。 对于掺镱激光增益介质,E0通常接近零声子跃迁的光子能量,即两个流形的最低子能级之间的跃迁。
McCumber分析的结果对于激光晶体通常相当准确。 然而,稀土掺杂激光玻璃的精度要差得多,特别是在展宽均匀的情况下[4]。
McCumber关系非常有用,例如,用于评估激光跃迁长波长侧的弱吸收截面。 从发射截面计算吸收截面比直接测量弱吸收要精确得多。 此外,本征荧光的光谱形状可以从吸收光谱计算出来。 当直接荧光测量受到高掺杂样品中的重吸收或激发态吸收的影响时,这可能是有利的。
参考文献
[1] D. E. McCumber, “Einstein relations connecting broadband emission and absorption spectra”, Phys. Rev. 136 (4A), A954 (1964), doi:10.1103/PhysRev.136.A954
[2] J. N. Sandoe et al., “Variation of Er3+ cross section for stimulated emission with glass composition”, J. Phys. D 5 (10), 1788 (1972), doi:10.1088/0022-3727/5/10/307
[3] W. J. Miniscalco et al., “General procedure for the analysis of Er3+ cross-sections”, Opt. Lett. 16 (4), 258 (1991), doi:10.1364/OL.16.000258
[4] M. J. F. Digonnet et al., “Fundamental limitations of the McCumber relation applied to Er-doped silica and other amorphous-host lasers”, IEEE J. Quantum Electron. 38 (12), 1629 (2002), doi:10.1109/JQE.2002.805111
[5] R. M. Martin and R. S. Quimby, “Experimental evidence of the validity of the McCumber theory relating emission and absorption for rare-earth glasses”, J. Opt. Soc. Am. B 23 (9), 1770 (2006), doi:10.1364/JOSAB.23.001770



