定义
激光束和谐振器模式或波导模式的电场分布的精确空间匹配。
在许多情况下,有必要在空间上将激光束精确匹配到另一个光束或模式,以获得某种有效的耦合。 例如:
- 来自激光的光束必须耦合到光纤中。
- 激光束必须与被动光学谐振器匹配,该谐振器应充当空间和/或光谱滤光片(→模式清洁腔)。
- 对于注射锁定,主激光器的模式必须与从激光器的模式相匹配。
模态的必要匹配不仅意味着在强度分布方面创建良好的空间重叠,而且还意味着匹配光学相位分布。 换句话说,光束的波前将被匹配。 如果两个光束(具有相同光学频率)的复振幅分布在某个平面上匹配良好,则在进一步传播期间它们将保持良好匹配。
模式匹配可以通过使用合适的中继光学器件(通常是曲面镜或透镜的某种组合)来实现,前提是初始光束的光束质量接近衍射极限。
在数学上,模态匹配的质量可以用重叠积分来量化。 以下公式涉及这种重叠积分的平方,计算有关光功率的耦合效率:
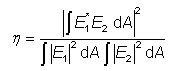
这里E1和E2是平面中的复杂电场,例如指激光束和谐振器或波导模式的场,积分跨越整个光束横截面。 该量在自由空间中传播期间保持不变。
类似的重叠积分可用于计算复模幅值。
如果来自可调频率单频激光器的光束击中对称的法布里-佩罗干涉仪,并且激光频率在谐振器的整个自由光谱范围内调谐,则透射光可用于分析模式匹配程度。 为了与腔模(通常是基本高斯模式)完美匹配,当满足谐振条件时,可以观察到谐振器的完全传输,而其他谐振(对应于其他谐振器模式)不能被激励。



