定义
基于光学技术的温度传感器,例如带光纤布拉格光栅的温度传感器。
光学温度传感器是基于光学技术的温度传感器 - 在大多数情况下,基于光纤。 它们可以基于不同的操作原理,如下所述。
有替代技术,特别是电子温度传感。 然而,光学温度传感器可以提供重要的优势。 它们可以在非常宽的温度范围内工作,对电磁干扰不敏感,并且不需要电缆(这对于需要使用绝缘材料的某些高压应用很重要)。 请参阅下面有关光学温度传感器应用的段落。
光学温度传感器的工作原理
基于光纤布拉格光栅的点传感器
许多用于测量温度的光纤传感器都基于光纤布拉格光栅(FBG)。 工作原理基本上基于温度影响布拉格波长的事实,即峰值反射率的波长。 温度变化ΔT和应变ε引起的布拉格波长变化为[4]:
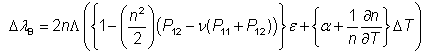
两种不同效应的组合决定了温度敏感性:热膨胀(用热膨胀系数α量化)和折射率的变化。
使用光电解调仪,将光发送到光栅传感器并分析反射光以确定应变量。 例如,外腔二极管激光器适合作为光源。
为了测量某些物体的温度,需要将基于FBG的传感器连接到组件上,使其获得相同的温度。 一些传感器用胶水、螺钉或类似方式连接,而另一些则嵌入某些材料中。
如上式所示,这种光栅的布拉格波长对机械应变也很敏感。 因此,需要注意测量信号是否真正反映了温度并且不受应变的影响。 然而,最简单的方法(可能需要一些小心)是安装光栅,使其保持松动并且不会拉紧。
如何区分温度和应变效应?
另一种可能性是将光栅暴露在温度和应变下,但采用某种方法来分离这两种效应。 例如,可以使用两种非常不同的询问波长(例如在0.8μm和1.5μm区域),导致应变和温度响应的比率不同。 通过这些技术,人们可以同时测量温度和应变。
请注意,通过光波长对温度进行编码使得此类传感器对其他参数不敏感,例如沿光纤的光功率损耗或解调仪的输出功率。
基于FBG的传感器的温度分辨率可以优于0.1 K;它基本上受到波长测量精度的限制。 对于 0.1 K 的温度分辨率,需要大约 1 pm = 0.001 nm 的波长分辨率。
准分布式传感器
准分布式传感器可以以经济的方式实现。
基于FBG的传感器技术的一个非常吸引人的特点是,可以在长光纤中制造具有许多此类光栅的准分布式传感器,并使用单个解调仪,该解调仪可以通过某种多路复用来解决所有不同的光栅。 来自不同光栅的信号可以用不同的方式区分:
- 解调仪可以发出光脉冲(例如纳秒或皮秒持续时间)并监控信号的到达时间(时分复用,TDM),由于光栅之间的光纤传播时间延迟,光栅的到达时间不同。
- 或者,不同的光栅可以具有不同的布拉格波长,因此可以通过将询问激光器调整到其波长(波分复用,WDM)来解决每个光栅。 除了激光,还可以将宽带光源(例如超发光二极管)与某种光谱仪结合使用,例如与可调谐法布里-佩罗滤光片或基于衍射光栅和CCD传感器阵列的设备结合使用。
还可以将这两种技术结合起来,实现包含更多点传感器(可能超过100个)的WDM/TDM系统。
与使用许多独立传感器相比,这种多点传感器的成本可以低得多,因为传感器和电缆的安装得到了简化,可以使用单个解调仪。
干涉光纤布拉格光栅传感器
在某些情况下,人们使用一对布拉格光栅形成法布里-佩罗干涉仪,其中通过共振频率的偏移来测量光栅之间光纤中的温度。 当使用具有不同布拉格波长的光栅时,可以再次在一根光纤中使用这种类型的多个传感器。 或者,可以测量一根长纤维中的平均温度。
基于微法布里-佩罗的传感器
人们可以构建小型法布里-佩罗干涉仪,其中小镜距(例如50μm)受某些材料热膨胀测量的温度的影响。 因此,峰值透射波长将指示温度。 代替透射,可以监测共振中的反射率下降。 探头灯端反射光可以通过单模光纤发送,以获得最大的便利性。 由于光纤仅用于传输光,而不用于实际传感器,因此该技术称为外在光纤传感器 - 与光纤本身充当传感器的固有传感器相反。
Micro-Fabry-Pérots可以以不同的方式生产,例如通过某些机械部件(例如微管)在两个光纤末端之间保持气隙,或者通过使用两个反射的熔接,例如通过在光纤末端施加介电涂层。
Micro-Fabry-Pérot传感器可以在比基于FBG的传感器更高的温度下工作,其中可能会发生光栅退火。 另一方面,在一根光纤中使用多个这种类型的传感器并不容易。
基于瑞利散射的分布式温度传感器
分布式光纤温度传感器可以用普通的单模光纤实现,不包含光纤布拉格光栅等任何特殊结构。 在许多情况下,人们使用在1.5μm光谱区域内运行的电信光纤。
一种可能性是利用光纤中的瑞利散射。 这是由于光纤的微观变化引起的线性散射,主要是折射率的波动。 然而,不幸的是,普通光纤中的瑞利散射仅表现出微弱的温度依赖性。 这对于液芯光纤来说要好得多,然而,液芯纤维的应用不太实用。 因此,人们主要使用非线性散射机制,如下所述。
基于拉曼散射的分布式温度传感器
对于较长光纤的温度传感,通常使用基于自发拉曼散射的技术。 人们利用了这样一个事实,即反斯托克斯与斯托克斯散射光功率的比率在很大程度上取决于温度:
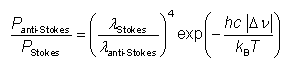
其中Δν是泵浦光的斯托克斯光和反斯托克斯光的所用频率偏移的大小。 用于二氧化硅纤维和波数偏移为 ±400 cm 的测量−1,该比率为≈0.15,温度依赖性为≈0.8%/K[3]。
询问器需要将短泵浦脉冲发送到光纤中,例如持续时间为几纳秒,然后检测背向散射光。 在这里,必须滤除瑞利散射产生的最强背散射分量,并且需要测量刚好高于和略低于泵浦波长的波长分量的功率(偏移为几十纳米),以确定功率比,根据上面的方程,功率比取决于温度。 为了获得空间分辨率,必须对功率测量进行时间解析。 例如,当光在1 ns内传播超过大约20 cm时,使用10 ns脉冲,可以实现1 m量级的空间分辨率。 (请注意,系数 2 来自光需要双向传播的事实。)
泵浦脉冲可以用脉冲半导体激光管产生,为了提高测量的灵敏度,它们可以在进入传感器光纤之前通过光纤放大器发送。 检测可以使用雪崩光电二极管完成。 解调仪可能必须对光纤中散射光的波长相关传播损耗进行校正。
这种温度传感器系统可以处理长长的光纤,可能长达数十公里。 空间分辨率通常为 1 m 量级,温度分辨率可达 1 K 量级。 例如,这种性能非常适合监测石油和天然气管道。
基于布里渊散射的分布式温度传感器
代替拉曼散射,可以使用布里渊散射。 在这里,温度依赖性有不同的起源:折射率和声速的温度依赖性决定了布里渊频移的大小。
当使用自发布里渊散射时,一个挑战是自发散射速率比拉曼散射弱得多,同时频率偏移要小得多,因此更难滤除瑞利散射光。 然而,通过使用受激布里渊散射可以大大提高灵敏度。 该方法称为布里渊光学时滞分析(BOTDA)。 在这里,使用额外的弱连续波探头光束,其传播方向与皮秒脉冲相反。 它的光学频率选择略低于脉冲频率。 然后将探头光束放大到脉冲和探头光束之间的光学频率差与局部布里渊位移(取决于应变和温度)重合的位置。 (或者,当探头光束的频率高于脉冲频率时,可以获得探头光束的非线性损耗。 这种测量是用可变的光学频率差进行的,通过结合这些数据,可以有效地获得布里渊频率与位置的映射。
红外温度传感器
温度传感器也可以基于测量物体发出的热辐射强度。 通常,人们使用一种红外探测器测量红外辐射的强度,该探测器对波长(例如照明)的光敏感。 这种测量原理可用于点传感器,也可用于成像设备。 有关更多详细信息,请参阅有关热成像的文章。
光学温度传感器的应用
光学温度传感器广泛用于工业加工厂、桥梁、隧道、矿山、建筑物、石油和天然气管道以及输电线路等技术设施的测量。 例如,它们可用于可靠地识别异常情况,例如火灾引起的温度升高。 使用长光纤进行分布式传感的能力通常也非常重要。 有时,人们可以从同时测量应变中受益。
参考文献
[1] J. P. Dakin et al., “Distributed optical fiber Raman temperature sensor using a semiconductor light source and detector”, Electron. Lett. 21 (13), 569 (1985), doi:10.1049/el:19850402
[2] A. H. Hartog et al., “Distributed temperature sensing in solid-core fibres”, Electron. Lett. 21 (23), 1061 (1985), doi:10.1049/el:19850752
[3] A. D. Kersey, “A review on recent developments in fiber optic sensor technology”, Opt. Fiber Technol. 2, 291 (1996), doi:10.1006/ofte.1996.0036
[4] A. D. Kersey et al., “Fiber grating sensors”, IEEE J. Lightwave Technol. 15 (8), 1442 (1997), doi:10.1109/50.618377
[5] Y. J. Rao, “Recent progress in applications of in-fibre Bragg grating sensors”, Optics and Lasers in Engineering 31, 297 (1999), doi:10.1016/S0143-8166(99)00025-1
[6] B. Lee, “Review of the present status of optical fiber sensors”, Opt. Fiber Technol. 9 (2), 57 (2003), doi:10.1016/S1068-5200(02)00527-8
[7] F. M. Cox et al., “Opening up optical fibres”, Opt. Express 15 (19), 11843 (2007), doi:10.1364/OE.15.011843



