定义
在介质中实现高效非线性相互作用的一组技术。
许多相敏非线性过程,特别是参数过程,如倍频、和和差频生成、参数放大和振荡以及四波混合,都需要相位匹配才能高效。 从本质上讲,这意味着确保相互作用波之间的适当相位关系(用于最佳非线性频率转换)沿传播方向保持。 只有满足该条件,从不同位置对乘积波的振幅贡献在非线性晶体的末端都是同相的。 换句话说,一些相位失配应该接近于零,以获得有效的非线性相互作用。 例如,对于倍频与共线波束的I型相位匹配,相位失配由下式给出
哪里k1和k2分别是基波束和二次谐波束的波数。 无色散,k2 = 2 k1将保持,以便相位不匹配消失。 但是,如果不采取特殊措施(如下所述)来避免这种情况,色散通常会导致非零相位失配(图1)。
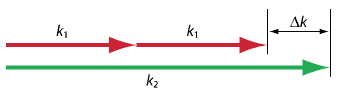
图1:二次谐波产生的相位失配。 由于色散,二次谐波的波数是基波的两倍多。 这可以避免,例如,通过在双折射晶体中选择不同的偏振(→双折射相位匹配)。
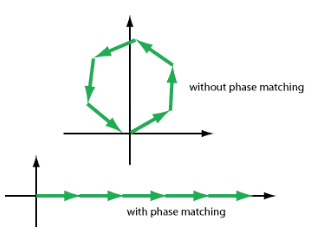
图2:添加晶体不同部分的振幅贡献。只有相位匹配,才能实现高转换效率。
图2说明了相位失配如何保持较低的效率。 在这里,箭头说明了对应于非线性晶体不同部分对谐波的复振幅贡献的相量。 只有实现相位匹配,这些贡献才会建设性地加起来,并实现高功率转换效率。 否则,能量转移的方向会根据相互作用波之间相位关系的变化而周期性地变化(在通过晶体的过程中可能变化数千次)。 然后能量在波之间振荡,而不是在恒定的方向上传递。 对功率转换的影响如图3所示。
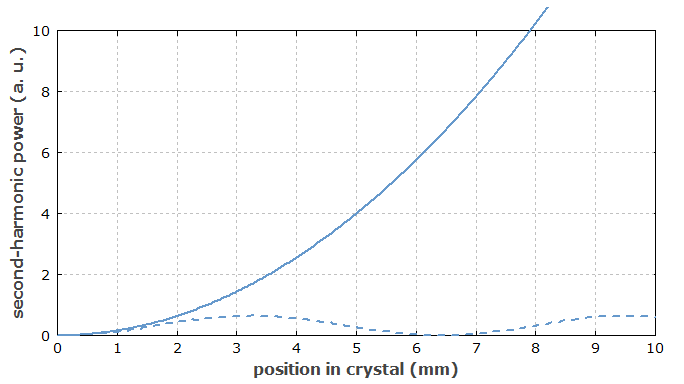
图3:晶体中二次谐波功率沿传播方向增长,假设泵浦强度恒定。 实线:相位匹配的情况下,功率与传播距离的平方成正比。 虚线曲线:非相位匹配情况,二次谐波功率在零和小值之间振荡。
在倍频器中,能量传输的方向由项的复相决定E12E2* 这里E1是基波的复电场幅值和E2二次谐波的谐波。 星号表示复杂的共轭。 相位匹配条件k2 = 2 k1暗示术语的阶段E12E2* 沿传播方向保持不变。 对于和频率生成过程,或在非简并光学参量振荡器中,相应的术语为E1东2东3*,相位匹配条件为k3 = k1 + k2.
对于倍频器或光参量放大器等器件,需要主动安排相位匹配。 另一方面,光参量振荡器可以自动选择其信号波长,从而实现相位匹配。因此,波长调谐可以通过影响相位匹配条件来实现,例如通过温度变化或角度调整。
相位匹配曲线
当晶体温度在最佳点附近变化时,相位失配,因此转换效率也会发生变化,如图4所示。 获得高转换效率的温度范围与晶体长度成反比。 它还取决于所涉及的折射率的温度依赖性。 类似的关系也适用于其他非线性变频过程。
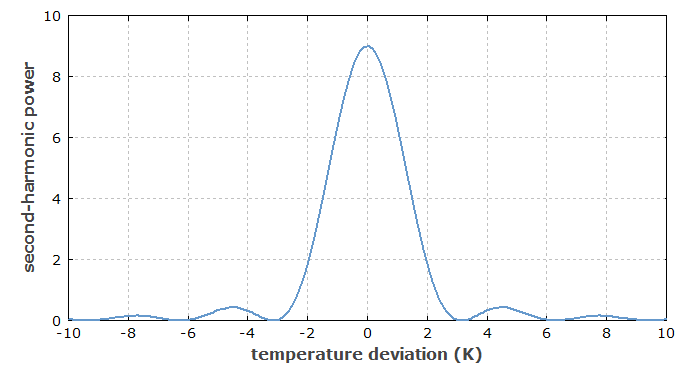
图4:二次谐波功率与温度与最佳点的偏差,假设晶体中的温度分布均匀,泵浦强度恒定(转换效率低)。
例如,当晶体的角取向发生变化时,可以获得类似的曲线。
相位匹配曲线实际上不需要如图4所示那样对称。 例如,如果晶体端面的晶体温度低于晶体中间,则变得不对称。 可以根据测量的相位匹配曲线量化晶体烘箱中的温度均匀性。 基于这些数据,可以估计是否可以提高转换效率,例如通过使用更长的晶体。
相位匹配技术
在非线性晶体中实现相位匹配的常用技术是双折射相位匹配,其中利用双折射来消除相位失配。 此技术有多种变体:
- I型相位匹配意味着,例如,在总和频率生成中,两个基波束具有相同的极化,垂直于总和频率波的极化。 相反,在II型相位匹配中,两个基本光束具有不同的偏振方向;当双折射相对较强(在I型方案中过度补偿色散)和/或相速失配较小时,这可能是合适的。 I型和II型之间的区别同样适用于倍频,以及简并或非简并参数放大等过程。 不同的偏振排列可能具有不同的实际意义,例如对于几个非线性转换级的组合,或腔内倍频。
- 临界相位匹配意味着使用晶体(或光束)的角度调整来找到相位匹配配置,而在非临界相位匹配中,所有偏振方向都沿晶体轴,并且角位置不是敏感参数。
- 所有涉及光束的波矢量可能具有相同的方向(共线相位匹配)或不同的方向(非共线相位匹配),但是,生成光束的矢量和等于乘积光束的波矢量。 一种特殊情况是消色差相位匹配,其中至少一个相互作用的波束是角度分散的,以便信号的每个频率分量都正确相位匹配。
准相位匹配是一种非常重要的特殊技术,其中不会发生实相位匹配,但在非线性的符号(或强度)呈周期性变化的晶体中仍可获得高转换效率。 非线性的这种周期性变化可以通过周期性极化等方式实现。 通常,所有涉及的波具有相等的偏振状态(因为不需要双折射),这种配置有时称为0型相位匹配。
相位匹配带宽和群速度失配
当实现相位匹配时,相互作用波的群速度通常仍然不匹配;存在一定的群速度失配,这限制了脉冲的相互作用长度和(对于给定的相互作用长度)实现相位匹配的频谱范围(称为相位匹配带宽)。 此外,相位匹配的光束角范围有限,特别是对于关键的相位匹配。 这个角度范围通常称为角相位匹配带宽。 有关更多详细信息,请参阅有关相位匹配带宽的文章。
相位匹配配置的选择:示例
对于任何给定的晶体和非线性相互作用(以参与波长为特征),可能存在多种相位匹配配置,其比较涉及许多重要性质。 哪种配置最合适,很大程度上取决于应用程序。
一个例子是LBO晶体中的总和频率生成,其中两个输入是1064和1535 nm,在628 nm处产生红色输出。 对于这种相互作用,存在三个关键相位匹配方案和两个非关键相位匹配方案,仅考虑共线相位匹配。 此外,具有临界相位匹配的情况仅限于20°C的晶体温度。 表 1 中列出了这些方案。
表 1:用于LBO中总和频率生成的各种相位匹配方案。
| 方案 | 非线性 | 走开 | GVM |
|---|---|---|---|
| XZ I(ee-o),θ= 88.0° | 0.85 pm/V | ρ1= −1.73 mrad ρ2= −1.82 mrad |
GVM13 = −0.30 fs/mm GVM23= +6.0 fs/mm |
| XZ II(eo-e),θ= 19.4° | 0.50 pm /V | ρ1= −15.1 mrad ρ2= −16.3 mrad |
GVM13 = +50.4 fs/mm GVM23= −30.3 fs/mm |
| YZ II(eo-o),θ= 41.1° | 0.51 pm /V | ρ1= −9.27 mrad | GVM13 = −74.6 fs/mm GVM23= +51.9 fs/mm |
| X / ZZY在13.6°C | 0.85 pm /V | – | GVM13 = −0.29 fs/mm GVM23= +6.0 fs/mm |
| Z / XYX 在 250 °C | 0.67 pm /V | – | GVM13 = +50.4 fs/mm GVM23= −29.5 fs/mm |
作为命名法的一个例子,临界方案XZ I(ee-o),θ= 88.0°意味着光束在XZ平面上以88.0°的角度传播到Z轴。 两个输入都具有非凡的(e)极化(I型),而乘积波具有普通(o)极化。 作为II型非临界方案的一个例子,以Z / XYX为例,其中光束在Z方向上传播并在X(1535 nm),Y(1064 nm)和X(628 nm)方向上偏振。
重要的是要认识到,相位匹配配置的选择也会影响非线性的有效强度,因为它决定了所涉及的电场相对于晶体轴的方向。 有些配置可以提供,例如,大增益带宽,但由于有效非线性非常弱,因此几乎无法使用。
原则上,非临界方案X/ZZY应提供最佳性能,具有最高的非线性度且无空间走偏。 然而,临界方案XZ I(ee-o)实际上非常相似:从非临界方案X / ZZY开始,只需将晶体旋转2°即可在20°C而不是13.6°C下获得相位匹配。 由于光束方向接近X轴方向,因此走线非常弱。
在需要II型方案的情况下(例如,当输入光束已经共线但具有正交偏振方向时),可以考虑方案YZ II(eo-o),即使方案XZ II(eo-e)的较低群速度失配对于超短脉冲可能更有利,因为色散脉冲展宽减少。
群速度不匹配(GVM),例如某些泵浦和信号波之间的不匹配(GVM)对于超短脉冲的转换可能很重要,这与相位匹配带宽有关。 请注意,不同方案之间的GVM值差异很大,这表明仅选择材料并不能确定此问题的重要性。 对于每个特定的相位匹配方案,都需要找到最佳的晶体长度(特别是对于超短脉冲)和光束腰。
显然,拥有可以系统地识别给定非线性相互作用的所有可能的相位匹配配置的软件非常有用,例如,基于所有相关波折射率的塞尔迈尔方程。 在此基础上,可以选择最合适的方案,同时考虑到对要设计的转换装置的具体要求。
光纤中的相位匹配
光纤也表现出光学非线性,其中一些的影响也受到相位匹配的限制。 例如,交叉相位调制、四波混合和参数放大可能是这种情况,但不是自相位调制,其中涉及的所有光子具有相同的波长,以及拉曼散射。 当一个人正在处理一个χ(3)非线性,相关的物理过程和方程与非线性晶体中的相互作用有些不同。 另一个复杂因素是相位匹配通常受到克尔效应的显着影响:由此产生的强度依赖性折射率也使相位匹配关系与强度相关。
大多数纤维没有大量的双折射。 因此,相位匹配在很大程度上由色散特性控制。 这些可以通过所使用的光纤设计在很大程度上进行修改 -通过光纤芯的折射率分布,如果是光子晶体光纤,则通过在光纤横截面上适当放置气孔。
另一个可能的并发症与沿纤维的色散波动有关。 这种波动可能是由芯径的波动引起的,例如,可能是由纤维制造过程中的波动引起的。 当然,重要的不仅仅是沿光纤的总群延迟色散,而是沿光纤的群速度色散或多或少是恒定的。 因此,具有不同色散波动量的不同纤维的结果可能大不相同。 不幸的是,用空间分辨率测量色散并不容易。
所解释的问题在超连续体生成的情况下尤为重要,其中应用了高光学强度,并且所采用的非线性过程的很大一部分受到相位匹配的影响。
参考文献
[1] P. D. Maker et al., “Effects of dispersion and focusing on the production of optical harmonics”, Phys. Rev. Lett. 8 (1), 21 (1962), doi:10.1103/PhysRevLett.8.21
[2] M. V. Hobden, “Phase-matched second harmonic generation in biaxial crystals”, J. Appl. Phys. 38 (11), 4365 (1967), doi:10.1063/1.1709130
[3] R. Eckhardt and J. Reintjes, “Phase matching limitations of high efficiency second harmonic generation”, IEEE J. Quantum Electron. 20 (10), 1178 (1984), doi:10.1109/JQE.1984.1072294
[4] A. V. Smith et al., “Increased acceptance bandwidths in optical frequency conversion by use of multiple walk-off-compensating nonlinear crystals”, J. Opt. Soc. Am. B 15 (1), 122 (1998), doi:10.1364/JOSAB.15.000122; see also references therein
[5] A. M. Schober et al., “Broadband quasi-phase-matched second-harmonic generation of ultrashort optical pulses with spectral angular dispersion”, J. Opt. Soc. Am. B 22 (8), 1699 (2005), doi:10.1364/JOSAB.22.001699
[6] O. Isaienko and E. Borguet, “Generation of ultra-broadband pulses in the near-IR by non-collinear optical parametric amplification in potassium titanyl phosphate”, Opt. Express 16 (6), 3949 (2008), doi:10.1364/OE.16.003949



