定义
一种基于孤子脉冲的激光模式锁定机制。
对于飞秒脉冲的生成,孤子模式锁定是一种利用孤子效应的常用技术。它最初是为光纤激光器开发的,但是在脉冲能量和持续时间方面非常有限,后来应用于锁模体(具有准孤子脉冲)。
光纤激光器的孤子模式锁定
对于真正的孤子模式锁定,在所使用的光纤中具有孤子脉冲传播,其中色散和非线性的影响共同作用,使得总体上没有脉冲的时间拓宽,也没有其光谱的任何变化[2]。这种效果的平衡需要具有异常色散的纤维,这很容易实现,例如在1.5μm状态下,并且 - 尽管二氧化硅纤维的分散正常 - 在使用具有合适设计的光子晶体光纤时,也以1μm状态。只有启动和稳定模式锁定时才需要饱和吸收器,而脉冲整形基本上是通过色散和非线性效应完成的。或者,可以使用主动模式锁定。获得的脉冲可以具有很好的时间曲线sech2型几乎没有任何啁啾声,即具有高脉冲质量。
不幸的是,孤子锁模光纤激光器的性能非常有限。对于皮秒脉冲持续时间,典型单模光纤的孤子能量非常小(在皮焦耳状态下),因此也是可能的输出脉冲能量。(操作具有远低于增益饱和功率的腔内平均功率(即仅略高于激光阈值)的激光器也是有问题的。对于飞秒状态下较短的脉冲持续时间,原则上可以获得显着更高的脉冲能量,但随后孤子周期变得更短;一旦它太短(特别是对于长激光谐振器),循环脉冲由于每次往返的非线性相移太高而变得不稳定。在脉冲变得非常不稳定之前,人们可能会在光谱中观察到大量的Kelly边带,即脉冲质量的下降。
一种准孤子模锁定可以在激光谐振器内附加强色散元件来实现,使得孤子平衡由每个谐振器往返的整体色散和非线性度决定。然后可以获得更高的脉冲能量,但结合更长的脉冲持续时间。
已经为光纤激光器开发了更复杂的模式锁定技术,以获得更好的性能。通常,它们依赖于更复杂的脉冲整形过程。有关更多详细信息,请参阅有关锁模光纤激光器的文章。
大体积激光器的准孤子模式锁定
如上所述,虽然孤子模式锁定的概念对光纤激光器具有严重的局限性,但对于固态体激光器来说,它变得非常重要。在这里,总内腔色散被异常化,例如通过将棱镜对或色散镜插入激光谐振器中。可以得到适当的分散度和Kerr非线性平衡,可以获得准孤子脉冲;首先应该关心适当的非线性量(见下文),然后引入所需的异常色散量以进行色散补偿。由于色散和非线性在谐振器中不是平滑分布的,而是在某些地方(例如,激光晶体和色散镜或棱镜对)集留的,因此人们不会获得真正的孤子脉冲,而是准孤子脉冲,其中色散和非线性的平衡仅适用于每个谐振器往返的整体非线性和色散相移。如果每次往返的相移不太强,这种平衡是有效的。同样,需要一个饱和的吸收器来启动和稳定模式锁定,但脉冲持续时间可能远短于吸收器的响应时间。
准孤子条件意味着孤子模式锁定激光的某些缩放定律。例如,将激光谐振器中的色散增加四倍可以使脉冲能量加倍,而脉冲持续时间也会加倍,从而使峰值功率以及每次往返的非线性相移保持不变。
与激光谐振器中具有接近零色散的模式锁定方案相比,孤子模式锁定允许由于Kerr非线性而产生更强的非线性相移,否则会使脉冲不稳定。每个谐振器往返的最佳非线性相移通常在几十到几百毫里亚数之间:
- 非线性相移值过低会导致孤子脉冲整形相当弱,从而导致对其他影响的敏感性更强,例如可饱和吸收体的脉冲整形细节、有限的增益带宽等。对于以相对较长的脉冲工作的锁模固态体激光器,可能会发生这种情况。在该制度下,人们还经常需要不方便的大量异常尿道分散。
- 另一方面,太强的非线性相移会使脉冲不稳定,这是由于循环脉冲在长度尺度上的周期性干扰,其长度尺度不比孤子周期短多少。
在某些情况下,可以通过修改棱镜对棱镜的棱镜插入来调整腔内色散。然后,人们可以观察到一种情况,其中脉冲持续时间(对于固定泵功率和脉冲能量)与异常色散的总量成比例地变化。然而,当脉冲持续时间变得太短时,脉冲突然变得不稳定。最小可能的脉冲持续时间可以通过有限的增益带宽或过高的非线性相移来设置。例如,图1显示了脉冲持续时间如何随使用脉冲传播软件进行数值建模的激光器中的色散量而变化。对于足够强的色散,其依赖性几乎是线性的,但如果色散变得太弱,脉冲就会变得不稳定。
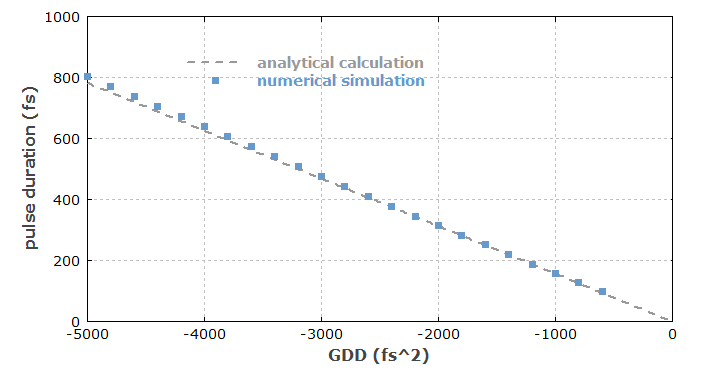
图 1:孤子锁模体积激光器的脉冲持续时间作为总腔内群延迟色散的函数。对于色散过低,脉冲不稳定;因此,图中缺少相应的标记。仿真是使用RP专业脉冲软件完成的;请参阅案例研究。
图2显示了在不稳定状态下数千次往返内光谱的演变(GDD = −400 fs2):
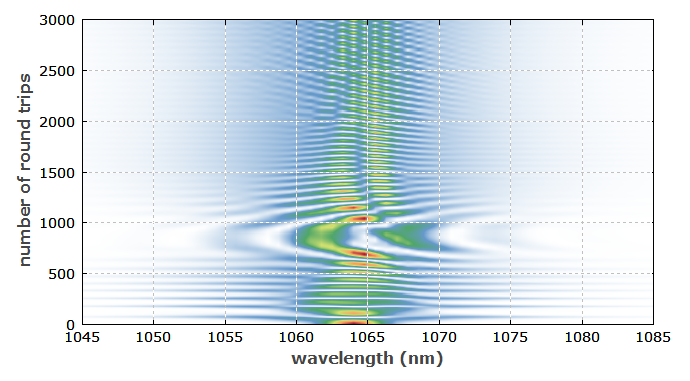
图 2:光谱在色散太弱的不稳定状态下演化。
对于锁模体激光器,孤子模锁定通常最适合低于1 ps的脉冲持续时间。对于远高于1 ps的脉冲持续时间,将需要不切实际的大量异常色散以及增强总非线性的可能元素。只有在低于10 fs的脉冲持续时间下,非线性相移通常会变得非常强(尽管使用相当短的激光晶体),以至于循环孤子的稳定性需要非常强的饱和吸收体。
当在适当的非线性相移状态下使用时,体激光器的孤子模式锁定通常允许良好的性能与高稳定性和非常高的脉冲质量相结合,即用于形状良好的接近带宽限制的超短脉冲和低啁啾。由于脉冲整形机制相对简单,这种激光器通常可以主要基于简单的解析方程进行设计,而不一定需要数值脉冲传播研究 - 除非需要研究其他细节,例如稳定性对设计细节的详细依赖性以获得尖端性能。
参考文献
[1] L. F. Mollenauer and R. H. Stolen, “Soliton laser”, Opt. Lett. 9 (1), 13 (1984), doi:10.1364/OL.9.000013
[2] F. M. Mitschke and L. F. Mollenauer, “Ultrashort pulses from the soliton laser”, Opt. Lett. 12 (6), 407 (1987), doi:10.1364/OL.12.000407
[3] J. D. Kafka et al., “Mode-locked erbium-doped fiber laser with soliton pulse shaping”, Opt. Lett. 14 (22), 1269 (1989), doi:10.1364/OL.14.001269
[4] I. N. Duling III, “All-fiber ring soliton laser mode locked with a nonlinear mirror”, Opt. Lett. 16 (8), 539 (1991), doi:10.1364/OL.16.000539
[5] T. Brabec et al., “Mode locking in solitary lasers”, Opt. Lett. 16 (24), 1961 (1991), doi:10.1364/OL.16.001961
[6] K. Tamura et al., “Soliton versus nonsoliton operation of fiber ring lasers”, Appl. Phys. Lett. 64, 149 (1994), doi:10.1063/1.111547
[7] F. X. Kärtner et al., “Stabilization of solitonlike pulses with a slow saturable absorber”, Opt. Lett. 20 (1), 16 (1995), doi:10.1364/OL.20.000016
[8] F. X. Kärtner et al., “Solitary pulse stabilization and shortening in actively mode-locked lasers”, J. Opt. Soc. Am. B 12 (3), 486 (1995), doi:10.1364/JOSAB.12.000486
[9] M. E. Fermann et al., “High-power soliton fiber laser based on pulse width control with chirped fiber Bragg gratings”, Opt. Lett. 20 (2), 172 (1995), doi:10.1364/OL.20.000172
[10] F. X. Kärtner et al., “Soliton mode-locking with saturable absorbers”, J. Sel. Top. Quantum Electron. 2 (3), 540 (1996), doi:10.1109/2944.571754
[11] A. B. Grudinin and S. Gray, “Passive harmonic mode locking in soliton fiber lasers”, J. Opt. Soc. Am. B 14 (1), 144 (1997), doi:10.1364/JOSAB.14.000144
[12] M. Santagiustina, “Third-order dispersion radiation in solid-state solitary lasers”, J. Opt. Soc. Am. B 14 (6), 1484 (1997), doi:10.1364/JOSAB.14.001484
[13] R. Paschotta et al.,“Passive mode locking with slow saturable absorbers”, Appl. Phys. B 73 (7), 653 (2001), doi:10.1007/s003400100726
[14] A. F. J. Runge et al., “The pure-quartic soliton laser”, Nature Photonics 14, 492 (2020), doi:10.1038/s41566-020-0629-6



