定义
光学谐振器的参数区域,其中谐振器在几何上是稳定的。
当激光谐振器(光学腔)的参数如臂长或谐振器中聚焦元件的屈光功率(反焦距)发生变化时,谐振器可以经过一个(对于环形谐振器)或两个(对于驻波谐振器)稳定区。
稳定性的概念来自纯几何分析中对光线的考虑:
- 稳定性意味着注入光学系统的光线即使在多次往返后,也将与轴保持有限的距离。
- 与此相反,对于不稳定的谐振器,无论光线从哪个方向开始,射线迟早会离开系统(除了沿系统轴线的传播)。
谐振器模式(用波动光学计算的自再现场配置)在稳定和不稳定状态下非常不同:
- 对于稳定的谐振器,如果可以忽略光学像差,则可以找到埃尔米特-高斯模式,或者具有略微不同性质的模式。至少低阶模式在光学元件(如反射镜)的边缘表现出可忽略不计的衍射损耗,除非这些元件太小。
- 在不稳定状态下,模式延伸到至少一个光学元件的边缘,这导致(a)大量的衍射损耗(即使使用大型光学元件)和(b)更复杂的模式强度分布。这种模式也更难计算。
通常,谐振器模式的性质在稳定区域内以及不同区域之间可能会有很大差异。
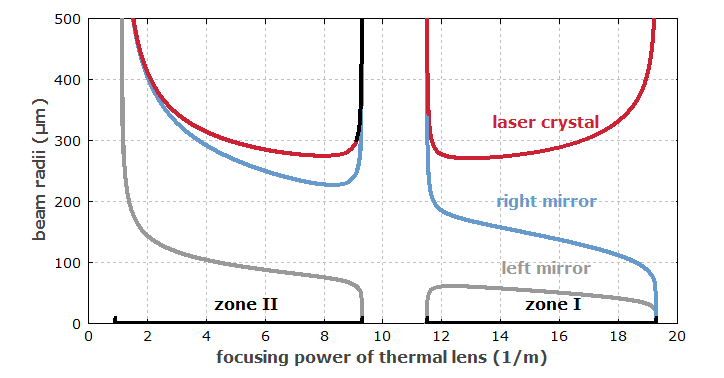
图 1:驻波激光谐振器的稳定区。曲线显示端镜和激光晶体中的光束半径是增益介质的热透镜的聚焦功率(屈光功率)的函数,该功率与泵浦功率大致成正比。根据Magni的说法,左边的区域是区域II,右边的区域是区域I。
大多数激光器的设计使其仅在稳定状态下运行。激光增益通常不足以克服不稳定状态下的大衍射损耗。然而,也有一些激光器设计有不稳定的谐振器 - 通常是具有高输出功率和高增益的激光器。
稳定区的属性
稳定区的详细特性对于谐振器设计问题非常重要,特别是作为激光设计的一部分,因为激光谐振器的特性对于激光性能至关重要。谐振器稳定区已经在大量文献中进行了探讨。
线性谐振器
Magni [2]的一篇论文对主要用于激光的线性谐振器进行了详细分析。下面讨论了一些重要的属性:
- 在线性谐振器稳定区的边缘,谐振器端镜处的光束半径可以发散或消失。
- 对于可变透镜,例如激光增益介质中的热透镜,可变透镜位置处的光束半径穿过稳定区域内的最小值(不一定靠近该区域的中间),并在稳定边缘发散。
- 线性谐振器的两个稳定区在可变透镜处具有相同的最小光束半径,但在其他方面却有很大不同。特别是,其中一个稳定区域(根据Magni称为区域II)具有稳定性边缘,其中两端镜上的模式大小发散。此时,谐振器的对准灵敏度也会发散,使得激光器在这样的点附近稳定工作难以实现:不仅反射镜倾斜,而且热透镜的不对称性,如泵浦对准期间可能发生的那样,严重影响激光模式的横向位置。另一个稳定区称为区域I,在对准灵敏度方面没有这种发散,并且在稳定性方面总体上总体上优于区域II。
- 就可变透镜的屈光度而言,稳定区的宽度是波长除以可变透镜处最小光束半径平方的两倍π倍。这意味着具有较大最小模态尺寸的谐振器不可避免地具有较窄的稳定区域。
- 线性谐振器的两个稳定区中只能观察到一个,例如,当可变透镜非常接近一端镜时(将区域I移动到具有非常强聚焦的状态),或者当两个稳定区合并形成宽度为两倍的单个区域时。
- 在光束轴周围没有圆形对称的情况下,水平和垂直方向的稳定区可以不同,并且不能重叠。
环形谐振器
与参考文献[2]中的线性谐振器类似,参考文献[3]提出了环形谐振器的分析。它们具有更简单的性质,但在许多方面与线性谐振器相似:
- 环形谐振器只有一个稳定区。
- 在稳定区的两个边缘,模式半径发散。然而,只有在其中一条边上,对准灵敏度也会发散,而在另一条稳定边上则达到最小值。
- 热透镜的最小模式尺寸再次决定了稳定性区域的屈光功率宽度,但该宽度是线性谐振器的两倍。
与线性谐振器的差异与以下事实有关:在环形谐振器中,激光束每次往返仅通过热透镜一次,而不是线性谐振器的两倍。
谐振器设计的结果
这些特性对激光谐振器设计(特别是对于固态体激光器)的一些影响将在以下简短讨论中讨论:
- 高功率固态激光器通常在增益介质中设计为相对较小的最小模式尺寸,否则稳定区将太窄,并且激光器只能在狭窄的泵浦功率范围内工作。然而,这样做的结果是,激光器将在多种横向谐振器模式下振荡,因此不会产生衍射极限输出光束。
- 为了稳定地操作具有衍射极限输出(高光束质量)的激光器,通常最好在增益介质中以最小模式尺寸在靠近点的位置工作,当然,设计谐振器时应使该模式与泵浦强度分布大致匹配。这样的操作点将热透镜聚焦功率的微小变化的灵敏度降至最低。
- 在稳定区I中操作激光器也是可取的,以便将对准灵敏度降至最低。有一个系统的程序来找到一种谐振器设计,该设计在所需稳定区的最小光束半径下工作,同时满足其他要求,例如合适的最小模式尺寸。
参考文献
[1] S. De Silvestri et al., “Novel stability diagrams for continuous-wave solid-state laser resonators”, Opt. Lett. 11 (8), 513 (1986), doi:10.1364/OL.11.000513
[2] V. Magni, “Multielement stable resonators containing a variable lens”, J. Opt. Soc. Am. A 4 (10), 1962 (1987), doi:10.1364/JOSAA.4.001962
[3] S. De Silvestri et al., “Rod thermal lensing effects in solid-state laser ring resonators”, Opt. Commun. 65 (5), 373 (1988), doi:10.1016/0030-4018(88)90106-X
[4] V. Magni et al., “Recent developments in laser resonator design”, Opt. Quantum Electron. 23, 1105 (1991), doi:10.1007/BF00619980
[5] N. Hodgson and H. Weber, Laser Resonators and Beam Propagation, 2nd edn., Springer, Berlin (2005)



