定义
动态模式分解是由Peter Schmid在2008年开发的一种降维算法[1]。对于一组时空耦合的数据,DMD能够便捷的提取出空域分量对应的时域的变化过程(模式),这种模式都与固定的振荡频率和衰减/增长率相关。DMD被广泛的应用非线性力学的研究中,主要通过使用线性方程组来拟合非线性的动力学问题,继而进行研究。
假设我们有如下线性系统[2]:
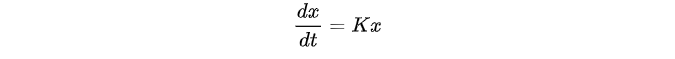
我们用简单的数值方法(比如欧拉法)将其离散化,可以得到:
![]()
此时,矩阵A就能够刻画这个线性系统的状态。但是由于xk以及xk+1可能会非常大,导致难以通过计算违逆的方式得到A的取值。此时这时候,如果我们先去对xk做奇异值分解(SVD),并且只保留前r阶,再去计算![]() 的特征值特征向量,就比直接计A的特征值特征向量,要快得多:
的特征值特征向量,就比直接计A的特征值特征向量,要快得多:
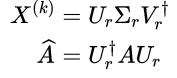
此时如果对![]() 进行特征值分解,那么分解得到的特征值就对应了DMD的谱,分解得到的特征向量就对应着DMD的模态。
进行特征值分解,那么分解得到的特征值就对应了DMD的谱,分解得到的特征向量就对应着DMD的模态。
参考文献
[1] https://en.wikipedia.org/wiki/Dynamic_mode_decomposition
[2] https://zhuanlan.zhihu.com/p/39304706



