定义
光束在透明介质中传播时，有自身引起的非线性效应导致光束聚焦。
由于克尔透镜效应，高光强的光脉冲在非线性介质中传播时会导致非线性的自聚焦效应：相比于弱光强的光束，其模场直径更小。其物理机制是基于具有正的χ(3)的非线性克尔效应。在这种情况下。在光轴上的光强较强，距离光轴越远的地方光强越弱，导致光束中间的折射率较高，光束边缘的折射率较低。这种折射率分布就像一个聚焦透镜一样，因而会产生聚焦效应。
另一种相关的效应是在具有负的负χ(3)非线性的介质中，会发生自散焦效应。在这种情况下克尔透镜的光束光轴上具有较低的折射率。
诸如热透镜效应也会产生自聚焦效应。
自聚焦的后果 自聚焦效应导致的光束半径的减小会增加光束的光强，从而进一步增强克尔透镜的效果，这种机制会导致非常高的光强，从而很可能会破坏光学介质（光学损伤）。当光功率高于临界功率时就可能会反生这样的失控效应，临界功率由以下公式给出：
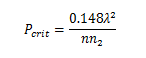
其中n2是非线性折射率，n为折射率。
值得注意的是，临界光功率不依赖于光束直径。较大的光束会产生一个较弱的克尔透镜，但由于其光束发散角更小使得其对透镜也更加敏感。但是，对于相同的功率，光束直径较大的光束需要较长的传播距离才会产生光学介质的损伤。对于石英，在1um波段，自聚焦效应会将光脉冲的峰值功率限制为4MW。在现阶段并没有什么方法可以使得光纤中的光功率可以超过以上的自聚焦临界功率。
此外，非线性折射率系数的值取决于脉冲脉宽。对于更短的脉冲，需要使用一个稍小的非线性折射率。这是因为没有足够的时间产生电致伸缩效应，并可能产生延迟的非线性响应。
在光纤中，其波导结构会决定光束的模式。然而自聚焦效应会减小有效模场面积（见图1）。在临界功率下（与空间体原件一样）模场面积接近零。
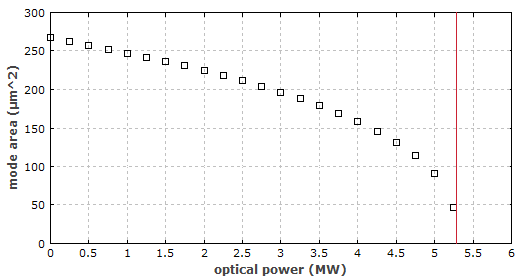图 1 数值计算的石英光纤中模场面积与光功率的关系图。非线性折射率取为2.2 · 10−20 m2/W。红线给出了自聚焦的临界功率。
均匀介质中的光束的功率恰好为自聚焦临界功率时，会产生光自陷效应（self-traping）[1]，此时光束的分布会在一段很长的距离内保持不不变，这是因为光束自身的发散恰好被非线性聚焦效应补偿。但是这种状态是不稳定的，即功率的微小偏差即会迅速偏离该状态。
高阶模式也会由于这种非线性作用变得不稳定。图2给出了一个例子，当功率为4MW的光束以LP11模式在光纤中传播时。当传播了10mm后，光束变成LP01和LP11的混合模式。
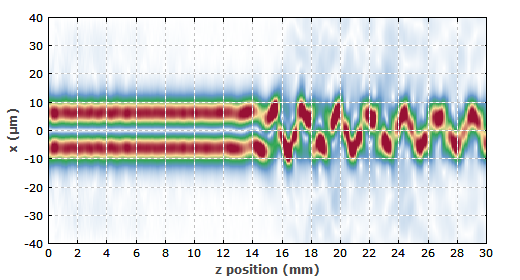图 2 以LP11模式入射的光束在xz平面上的光束分布图。
当光功率远远高于自聚焦临界功率时，会发生成丝（filamentation）现象，即光束会分解成几个具有较小功率的光束。最后的光束图案可能是随机的，但在某些情况下，它也有一个相当规则的结构。
当超短脉冲的脉宽与非线性特征时间同一量级或仅略大时，会发生一些不同的效应（瞬态自聚焦[2]）。
高光强（其对应功率小于自聚焦临界功率）导致的光束模场面积的变小可用于克尔透镜锁模激光器。光束面积的减小使得激光光束和泵浦光束具有更好的重叠或者使得激光在光阑处具有更小的损耗。在这两种情况下，这种效应形成了一种人造的可饱和吸收体。
自聚焦效应的另一个应用是用于对克尔非线性（参阅Z扫描测量）的大小进行测量。
需要注意的是级联的χ(2)非线性也会导致有效的χ(3)非线性，从而导致自聚焦或自散焦（负的χ(3)非线性）。
参考文献
[1] R. Y. Chiao, E. Garmire, and C. H. Townes, “Self-trapping of optical beams”, Phys. Rev. Lett. 13 (15), 479 (1964)
[2] Y. R. Shen, “Self-focusing: experimental”, Prog. Quantum Electron. 4, 1 (1975)
[3] J. H. Marburger, “Self-focusing: theory”, Prog. Quantum Electron. 4, 35 (1975)
[4] G. Cerullo et al., “Space-time coupling and collapse threshold for femtosecond pulses in dispersive nonlinear media”, Opt. Lett. 21 (1), 65 (1996)
[5] G. Fibich and A. L. Gaeta, “Critical power for self-focusing in bulk media and in hollow waveguides”, Opt. Lett. 25 (5), 335 (2000)
[6] R. L. Farrow et al., “Peak-power limits on fiber amplifiers imposed by self-focusing”, Opt. Lett. 31 (23), 3423 (2006)
[7] L. Dong, “Approximate treatment of the nonlinear waveguide equation in the regime of nonlinear self-focus”, J. Lightwave Technol. 26 (20), 3476 (2008)
[8] A. V. Smith et al., “Optical damage limits to pulse energy from fibers”, IEEE J. Sel. Top. Quantum Electron. 15 (1), 153 (2009)
[9] D. E. Laban et al., “Self-focusing in air with phase-stabilized few-cycle light pulses”, Opt. Lett. 35 (10), 1653 (2010)
[10] P. Whalen et al., “Self-focusing collapse distance in ultrashort pulses and measurement of nonlinear index”, Opt. Lett. 36 (13), 2542 (2011)
[11] R. Paschotta, tutorial on "Passive Fiber Optics", Part 11: Nonlinearities of Fibers
参阅：克尔效应、克尔透镜锁模、z扫描测量、B参数
