定义
光波在传播过程中,由于受到限制(即空间调制)时所发生的偏离直线传播规律的现象。
标量衍射理论即为一种解释衍射现象的近似理论,衍射理论要解决的问题是分析由光源发出的光波,受到衍射物体的限制后,在观察平面上造成的复振幅分布或辐照度分布。衍射孔径比波长大很多,观察点离衍射孔距离不近。
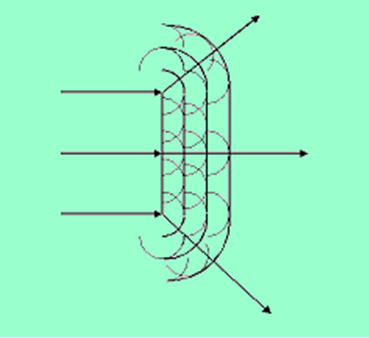
经典的标量衍射理论最初是1678年惠更斯提出的,他指出波面上每一点可看作次级球面子波的波源,下一时刻新的波前形状由次级子波的包络面决定。
 |
 |
图 1 惠更斯子波假设
惠更斯子波假设能预见光在通过简单孔径时的衍射现象,但它只能判断光的传播方向,不能定量计算。后来又出现了惠更斯-菲涅耳原理,最后不断完善形成了基尔霍夫衍射理论,略去推导过程,推导过程可以参考来源波动光学相关书籍,基尔霍夫衍射积分公式如下:
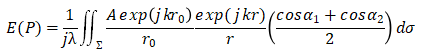
用基尔霍夫理论可以推导菲涅耳衍射公式:
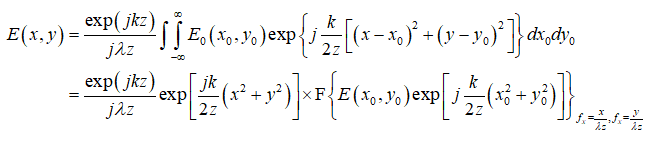
上式经过菲涅耳近似:

如果进一步对系统施加限制使得: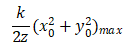
则衍射过渡到夫琅禾费衍射区,夫琅禾费衍射公式:
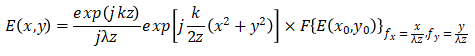
该式表明,除了一个与传播距离及观察面坐标有关的位相因子以外,观察平面上的衍射场分布正比于衍射屏透射光场分布的傅里叶变换,其振幅及变换的尺度与距离z有关。
夫琅禾费衍射与菲涅耳衍射的对比
夫琅禾费衍射区的条件苛刻,例:λ=632.8nm,Rmax=31mm,菲涅耳衍射区z >>1.2m,夫琅禾费衍射区要求 z >>6.3m,λ=532nm,夫琅禾费衍射区要求z >> 7.5m。
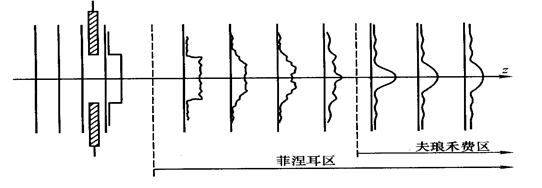
图 2 菲涅耳衍射区与夫琅禾费衍射区
二者关系:菲涅耳衍射区包括了夫琅禾费衍射区,夫琅禾费衍射是菲涅耳衍射的进一步近似。
以圆孔衍射举例说明:
圆孔透过率函数:
![]()
观察面复振幅分布:

观察面强度分布:


图 3 圆孔夫琅禾费衍射图样(即艾里斑)
衍射图样:光能重要集中在中央亮斑。周围是一些亮暗相间的圆环,当圆孔愈小,中央亮斑就愈大。
参考文献
[1] 吕乃光. 傅里叶光学[M]. 2016
[2] 苏显渝. 信息光学[M]. 2011
参阅:光波的数学描述、干涉



