模块度
Modularity Measure(模块化度量值），由Newman[1]等人提出，是目前常用的一种衡量网络中社区稳定度的方法。
理解1
假设网络被划分为k个社区，那么定义一个k×k的对称矩阵e，它的元素eij表示社区i和社区j之间的边的数量。矩阵的迹
，也就表示了在相同社区内节点之间的边集合。显然，社区划分的好，也就是社区内节点之间联系密集，那么该值就越高，这与我们通常对社区的认识是一致的。作者也指出，仅通过矩阵的迹这个值不能完全反应社区结构，因为如果把网络仅划分成1个社区的话，那么会导致Tre=1。因此又定义了一个值
，表示所有连接到社区i的边数量。于是，作者定义了一个模块度的概念：
||x||表示矩阵x的所有元素的和。
简单展开一下上面的公式更加清晰：
例如，如下图所示，10个节点，12条边，被分成3个社区：
根据上述定义，生成的社区矩阵为：
| 1 | 2 | 3 | |
| 1 | 3 | 0 | 1 |
| 2 | 0 | 3 | 1 |
| 3 | 1 | 1 | 4 |
模块度
理解2
其实， 模块度还有一种更加直白的理解：（落在同一组内的边的比例） 减 （对这些边进行随机分配所得到的概率期望）。理解这种算法前，需要先定义一些的内容：
假设网络有n个节点，有m条边，节点v的度表示为kv。
将网络的邻接矩阵表示为A，Avw = 0表示v和w之间没有边，Avw = 1表示有边。定义变量s，svw = 1表示v和w属于同一社区，svw = -1表示不在同一社区，那么可以用\delt_{vw} = \frac{1}{2}(s__{vw} +1)量化表示v和w是否在同一社区，如果是则等于1，不是则等于0。
那么上述模块度定义可以表示为：
表示在同一社区内的边的数量占所有边数量的比例， 乘以 1/2，是因为对每条边计算过两次。那么接下来，看一下期望是如何计算的：这里面用到了Configuration Models，大体意思就是，对网络的边进行随机分配，需要将每条边切断一分为二，切断的点我们称作末梢点(stub)，这样m条边就会产生
个末梢点，随机的将这
个末梢点进行连接，包括同一节点拥有的末梢点的自连接。这样可以保持每个节点原有的度不变的条件下，可以得到一个完全随机网络。
在该网络下，任意两点v、w连接边数的期望值是：
因此，节点v和w的实际边数与随机网络下边数期望之差为：
模块度最终可表示为：
定义 eij表示连接社区i和j的边的总数，
，ai表示连接社区i的边的总数，
，那么模块度可以表示为：
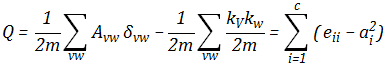
可以看到，虽然初始含义不同，但经过推导，模块度的公式(1)和公式(2)具有一致的表现形式，而且最终的结果非常简单。
参考文献
[1] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical review E, 2004, 69(2): 026113.
