定义
Marcenko-Pastur 分布(下文简称M-P分布)是随机矩阵理论的一个数学术语,也称作Marcenko-Pastur 定理,它被用来描述大型随机矩阵的特征值的分布规律。这个理论由乌克兰数学家Vladimir Marchenko 和Leonid Pastur在1967年给出了证明。详细定义如下:
如果 X 代表一个 m×n 的随机矩阵,里面每一行的元素都是来自于相互独立的随机变量,均值为0,方差σ2<∞,计:Yn = (1/n) XXT 为 X 的协方差矩阵,并且 λ1,λ2,……,λm是Yn的奇异值,也是 X 的特征值。那么,当矩阵m→∞而且m/n→λ∈(0,∞)时,这个协方差矩阵Yn将弱收敛于一个确定的分布,也就是参数为λ的M-P分布,概率密度如下式[1]:
![]()
其中![]()
实质
这个分布明确了一个无限大的随机矩阵(每一行都是独立的变量),其特征值服从的分布。换句话说,这个分布可以用来计算特征值来自于随机矩阵的概率,从而判断该特征值是否来源于一个每一行都独立的随机矩阵,因此很适合用在一些情境的零假设中。
应用
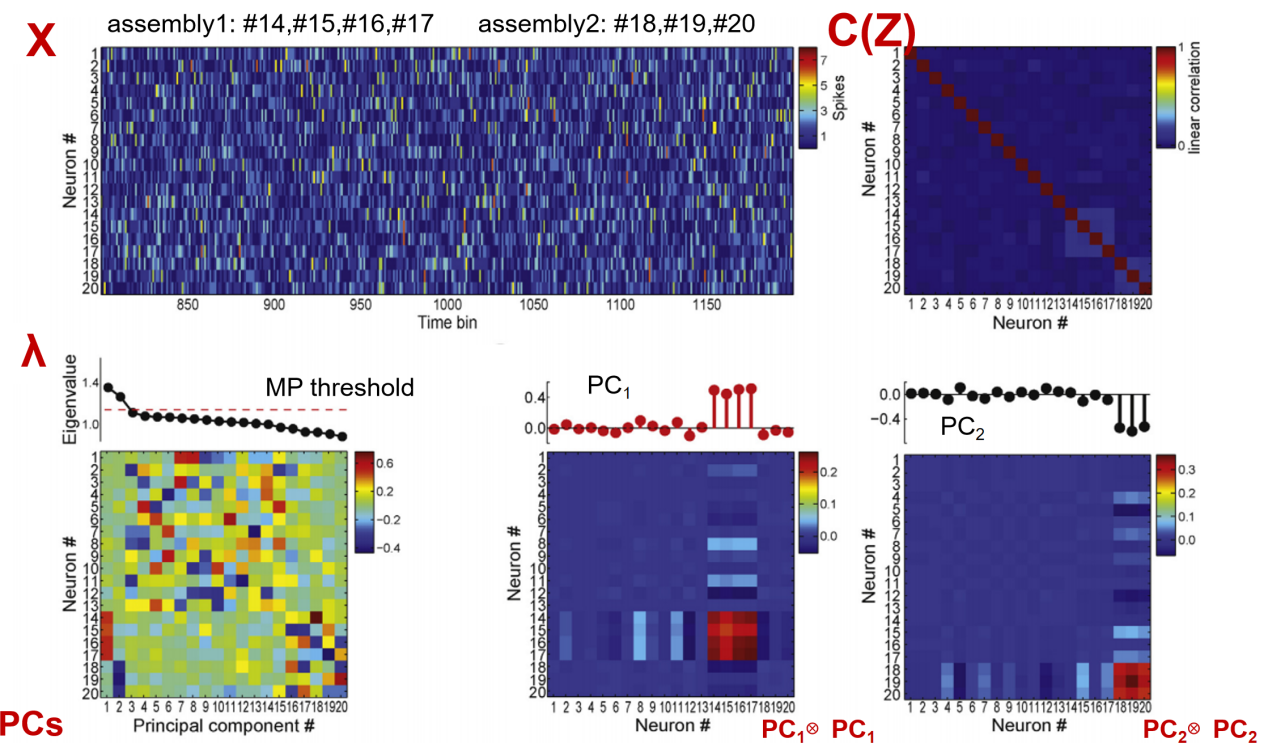
寻找神经元的潜在社群数量。首先,神经元的钙信号矩阵X,每一行代表一个神经元,每一列是该神经元的信号。如果神经元相互之间都独立,那么钙信号矩阵X的特征值将都满足M-P分布,也就是任何一个特征值都在M-P分布给出的特征值范围[λ-,λ+]内。然而,如果神经元之间存在n个社群(下图中n=2),那么这n个社群内的神经元不互相独立,从协方差矩阵C(X)上来看,则有n个明显的块,块内的神经元相互之间有很高的线性相关性,对于对应有n个特征向量PCs的特征值λ显著高于MP的右边界λ+ [2]。
代码实现:

参考文献
[1] Bryson, Jennifer, Roman Vershynin, and Hongkai Zhao. "Marchenko-Pastur law with relaxed independence conditions." arXiv preprint arXiv:1912.12724 (2019).
[2] Lopes-dos-Santos, Vítor, Sidarta Ribeiro, and Adriano BL Tort. "Detecting cell assemblies in large neuronal populations." Journal of neuroscience methods 220.2 (2013): 149-166.



