光属于电磁波(横波),其传播规律可以用电磁波理论来描述,可从麦克斯韦方程组推导出波动微分方程并验证其波动性(只适用于各向同性的均匀介质)。
波函数是用函数形式描述的光波,通常用E或U进行表示,光波本质是矢量波,但可分解为直角坐标系的三个分量,每一个分量可作为标量波处理。大多数光波是一维波和三维波,一维波是指沿一维方向传播且考察点位置坐标只需沿一维方向取值的光波,三维波是子三维空间中传播且考察点位置坐标在三维空间取值的光波。
一维波函数形式
波动微分方程形式如下:
![]() 其用来表示波函数的方程解写作:
其用来表示波函数的方程解写作:![]()
当一维波函数取正余弦函数的形式时称为一维简谐波,复杂波则可以分解为简谐波。此时的波函数表示为:
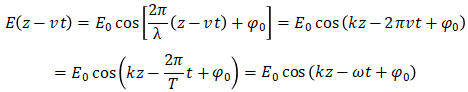
其中E0、![]() 分别表示振幅和相位。
分别表示振幅和相位。
简谐波的空间参量包括λ 、f、k。光波的空间周期为λ ,表示波形变化一个州市对应在空间传播的距离;f则定义为空间频率(也称波数),表示单位长度上波的周期数![]() ;v表征波传播的速度,v>0表示沿z轴的正向传播,v<0表示沿z轴的负向传播;k定义为空间角频率(也称传播数),
;v表征波传播的速度,v>0表示沿z轴的正向传播,v<0表示沿z轴的负向传播;k定义为空间角频率(也称传播数),![]() 。
。
简谐波的时间参量包括T、W。W为时间周期,表示波传播空间任一点的振动周期,![]() ;W为时间角频率,表示任一考察点处波的相位随时间的变化,
;W为时间角频率,表示任一考察点处波的相位随时间的变化,![]() 。
。
空间参量描述的是某时刻波的相位随空间坐标的变化,时间参量描述的是某考察点处的波的相位随时间的变化, 因此两组参量由波的传播速度相联系,即![]() 。
。
用复指数形式来表示光波便于运算(同时可将与空间坐标有关的因子和与时间相关的因子分离),一维简谐波的波函数常表示为复指数函数取实部的形式: 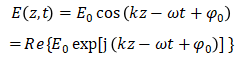
一般省去取实部的符号“Re”,一维简谐波的波函数直接表示为: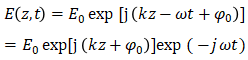
其中,![]() 称为波的复振幅。
称为波的复振幅。
三维波函数形式
光波在三维空间中传播, 确定空间考察点的位置需要用三维空间位置矢量![]() ,
,![]() ,用
,用![]() 代替z, 则波函数可写成
代替z, 则波函数可写成![]() 或
或![]() , 按照一维波函数的推导方式,可得三维波的波函数为:
, 按照一维波函数的推导方式,可得三维波的波函数为:

某一时刻t0具有相同相位值![]() 的点的位置轨迹(或集合)称为光波的波面或波前(wavefront)或等相位面。按照波面的不同,三维波可分为最基本的平面波和球面波,任何复杂波的基元是球面波和平面波,平面波对应于无限远处理想点源发出的波;球面波对应于有限远处理想点源发出的波,平面波可看作波面曲率半径趋于无限大时的球面波。
的点的位置轨迹(或集合)称为光波的波面或波前(wavefront)或等相位面。按照波面的不同,三维波可分为最基本的平面波和球面波,任何复杂波的基元是球面波和平面波,平面波对应于无限远处理想点源发出的波;球面波对应于有限远处理想点源发出的波,平面波可看作波面曲率半径趋于无限大时的球面波。
首先考虑平面波,波函数取正弦或余弦形式的三维平面波称为三维简谐平面波。

其复数形式为:![]()
三维简谐平面波各个时间参量的定义和性质与一维简谐平面波的完全相同,但空间参量有其特殊性,λ 是沿![]() 方向的空间周期,考察方向不同,空间周期也不同。同样,空间频率与空间周期一样也是考察方向的函数。fx、fy、fz又称为三维简谐波固有空间频率f的坐标轴分量, 且
方向的空间周期,考察方向不同,空间周期也不同。同样,空间频率与空间周期一样也是考察方向的函数。fx、fy、fz又称为三维简谐波固有空间频率f的坐标轴分量, 且![]() ,空间角频率的大小为
,空间角频率的大小为![]() 。
。
三维简谐平面波的复振幅:
![]()
注意,光波能量与其振幅的平方成正比,因此求光强I时常用![]() 表示。
表示。
再来看球面波,其等相位面时以点光源为中心,随距离的增大而逐渐扩展的通信球面,波函数取正余弦形式对应的球面波称为简谐球面波。
![]()
复指数表达式为:![]()
复振幅表示为:![]()
简谐球面波参量特点是其振幅(![]() )没有空间周期性且与传播距离成反比,但在r相同的球面上振幅仍然均匀相等,其中E0为波源的强度。
)没有空间周期性且与传播距离成反比,但在r相同的球面上振幅仍然均匀相等,其中E0为波源的强度。
参考文献
[1] 吕乃光. 傅里叶光学[M]. 2016
[2] 石顺祥,王学恩,马琳. 物理光学与应用光学[M]. 2014
参阅:干涉、衍射



