定义
球差是宽光来象差，仅是口径的函数[1]。
概述
球差是由于电磁透镜中心区域和边缘区域对电磁波会聚能力不同而造成的。远轴电磁波通过透镜时被折射得比近轴电磁波要厉害得多，因而由同一物点散射的电磁波经过透镜后不交在一点上，而是在透镜相平面上变成了一个漫射圆斑。球差是限制透镜分辨本领最主要的因素[2]。
分析
对于轴上物点，近轴光线的光路计算结果
和
与光线的入射高度
或孔径
无关，而远轴光线的光路计算结果
和
随入射高度 或孔径角
的不同而不同，如所示。
因此轴上点发出的同心光束经光学系统后，不再是同心光束，不同入射高度
的光线经过光学系统后交与光轴不同位置，相对近轴像点（理想像点）有不同程度的偏离，这种偏离称为轴向球差，简称球差，用
表示，起计算公式如式 1所示。
式 1
如图 1所示，由于共轴球面系统的对称性，含轴的各个截面内的成像光束结构均相同。在同一截面内，入射高度为
和
（或
、
）的光线相对光轴也是对称的。这样，通过系统后的成像光束是以光轴为旋转轴的非同心光束，所以计算球差时只需要计算子午面内光轴某一侧的不同入射高度的光线束即可。
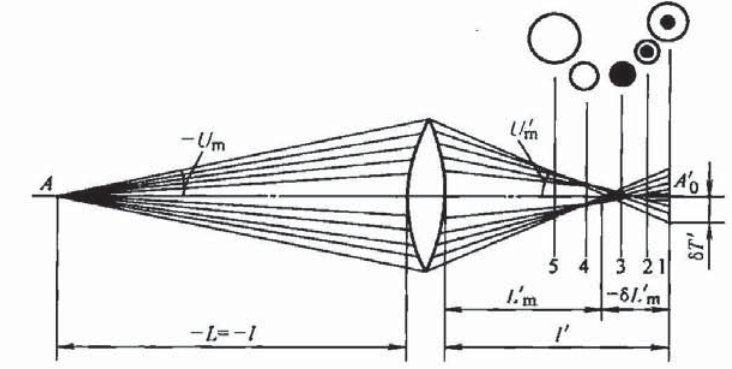
图 1 球差示意图[1]
由于球差的存在，在高斯像面上的像点已不是一个点，而是一个原型的弥散斑，弥散斑的半径用
表示，称作垂轴球差，它与轴向球差的关系如式 2所示。
式 2
球差是入射高度 或孔径角 的函数，球差随 或 变化的规律，可以由随 或 的幂级数表示。由于球差具有轴向对称性，当 或 变号时，球差 不变，这样在级数展开时，不存在 或 的奇次项；当 或 为零时，像方截距 等于 ，即球差为零，故展开式中没有常数项；球差是轴上点像差，与视场无关，故展开式中没有
或
项，所以球差可以表示如式 3所示。
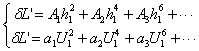式 3
展开式中第一项为初级球差，第二项为二级球差，第三项为三级球差。二级以上球差为高级球差。
、
、
分别为初级球差系数、二级球差系数、三级球差系数。大部分光学系统二级以上的球差很小，可以忽略。由此可知初级球差与孔径的平方成正比，二即球差与孔径的4次方成正比。当孔径较小时，主要存在初级球差；孔径较大时，高级球差增大。
光学系统的球差是由系统各个折射面产生的球差传递到系统的像空间后相加而得，故系统的球差可以表示成系统每个面对球差的贡献之和，即所谓的球差分布式。
球差矫正
如果把单正透镜和负透镜分别看作无数个不同楔角的光楔组成，则由光楔的偏向角公式（如式 4所示）可知，对于单正透镜，边缘光线的偏向角比靠近光轴光线的偏向角大，即边缘光线的像方截距 比近轴光线的像方截距 小。
式 4
根据球差的定义，单正透镜产生负球差。同理对于单负透镜，边缘光线的偏向角比近轴光线的偏向角大，但方向与单正透镜相反，所以单负透镜产生正球差。因此，对于共轴球面系统，单透镜本身不能矫正球差，正、负透镜组合则有可能矫正球差。
参考文献
[1] 郁道银. 工程光学(第2版)[M]. 机械工业出版社, 2006.
[2] https://baike.baidu.com/item/球差
