定义
吸收与透明介质折射率之间的数学关系。(有时会被错误的写为“Kramers–Krönig relations”)
在复解析函数理论中,函数的实部可以表示成虚部的积分形式,反之亦是如此。这一关系在线性和非线性光学中都用途广泛。应用到与频率有关的电介质方程ε(ω)中,得到:
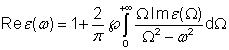
该方程是以Ralph Kronig和Hendrik Anthony Kramers命名的。其中Re ε(ω)与折射率有关,而Im ε(ω)则与吸收(或增益)有关。积分前面的符号是柯西主值,在进行数值积分时需要认真考虑。
而ε(ω)的虚部还满足另一个方程(这里未给出),由任意波长的折射率得到对某一波长的吸收。该方程实际中用处不多。两个方程合起来称为Kramers-Kronig色散关系。
还有另一种形式的Kramer-Kronig关系,指的是折射率n与强度吸收系数α的关系:
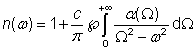
这两种形式并不直接相关,在第一种形式中被积函数的分子中包含一个因子Ω。
Kramers-Kronig关系的应用
通过Kramers-Kronig关系可以计算折射率分布,因此从与频率相关的损耗就可以得到介质的色散,可以在很大的光谱范围内测量。还有一个类似的关系式,可以由折射率计算吸收,但该关系并不常用,因为它很难在很宽的频率范围内测量折射率。
改进的Kramers-Kronig关系经常用在非线性光学中[3]。基本原理就是介质受到激发(例如,在半导体中产生载流子)引起的折射率变化与吸收的变化有关。由于只有在有限的频率范围内的吸收变化是比较重要的,因此相对容易测量。这一方法还可以应用于激光增益介质中,例如,计算光纤放大器中与激发能级有关的相位变化[4,5]。在稀土掺杂增益介质中,得到一定激光跃迁附近增益和损耗的变化是不够的,因为在紫外光谱区域的强吸收线也非常重要。
参考文献
[1] R. de L. Kronig, “On the theory of the dispersion of X-rays”, J. Opt. Soc. Am. 12 (6), 547 (1926)
[2] M. Beck et al., “Group delay measurements of optical components near 800 nm”, IEEE J. Quantum Electron. 27 (8), 2074 (1991)
[3] D. C. Hutchings et al., “Kramers–Kronig relations in nonlinear optics”, Opt. Quantum Electron. 24, 1 (1992)
[4] M. Montagna et al., “Nonlinear refractive index in erbium-doped optical amplifiers”, Opt. Quantum Electron. 27, 871 (1995)
[5] J. W. Arkwright et al., “Experimental and theoretical analysis of the resonant nonlinearity in ytterbium-doped fiber”, J. Lightwave Technol. 16 (5), 798 (1998)
[6] M. Sheik-Bahae, “Nonlinear optics basics: Kramers–Kronig relations in nonlinear optics”, in Encyclopedia of Modern Optics (eds. B. Guenter and D. Steel), Academic Press, London (2004)
[7] J. D. Jackson, Classical Electrodynamics, 2nd edn., John Wiley & Sons, Inc., New York (1975)
参阅:色散、折射率



