在介绍群卷积之前,首先对群的概念进行说明。
在数学中,群被定义为一个具有二元运算的集合[1],该运算能够将群中的任意两个元素组合成为第三个元素。当该集合及二元运算满足群公理的四个条件时,便是一个群。群公理的四个条件分别为:封闭性、结合性、单位元及逆元。接下来我们以Cayley图[2]的形式对群进行更形象的说明。
对于字母F,定义两种旋转操作:90度顺时针旋转r、水平翻转s,对应的效果为![]() ,
,![]() 。根据两种旋转操作,能够得到如下Cayley关系图。
。根据两种旋转操作,能够得到如下Cayley关系图。
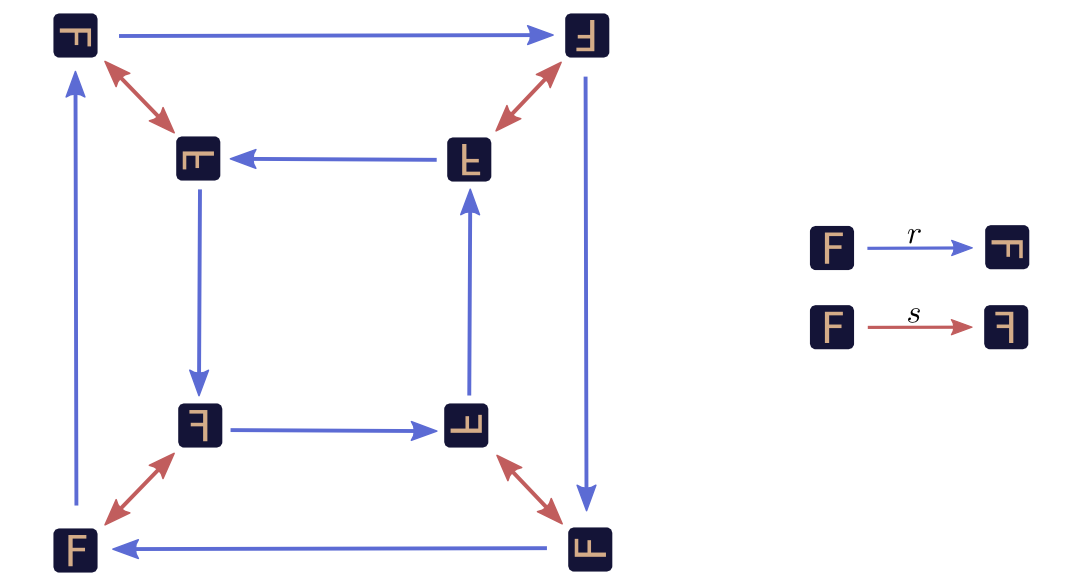
图 1 Cayley关系图1
因为![]() ,且
,且![]() ,所以有
,所以有![]() 。可根据图1得到如下关系图,其中e为恒等变换,即
。可根据图1得到如下关系图,其中e为恒等变换,即![]() 。
。
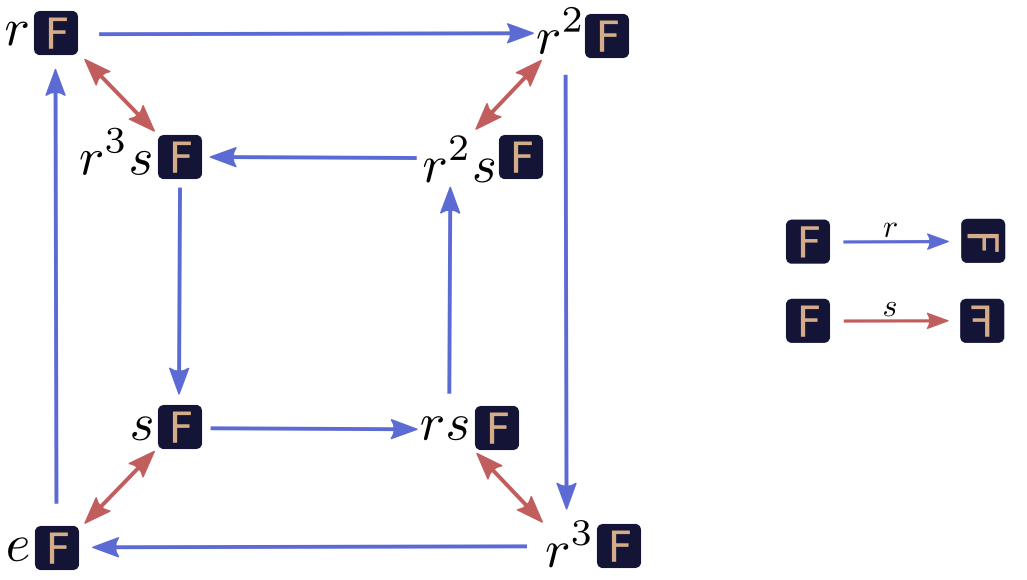
图 2 Cayley关系图2
为了更清楚地说明变换之间的关系,去掉F仅保留如下关系图。
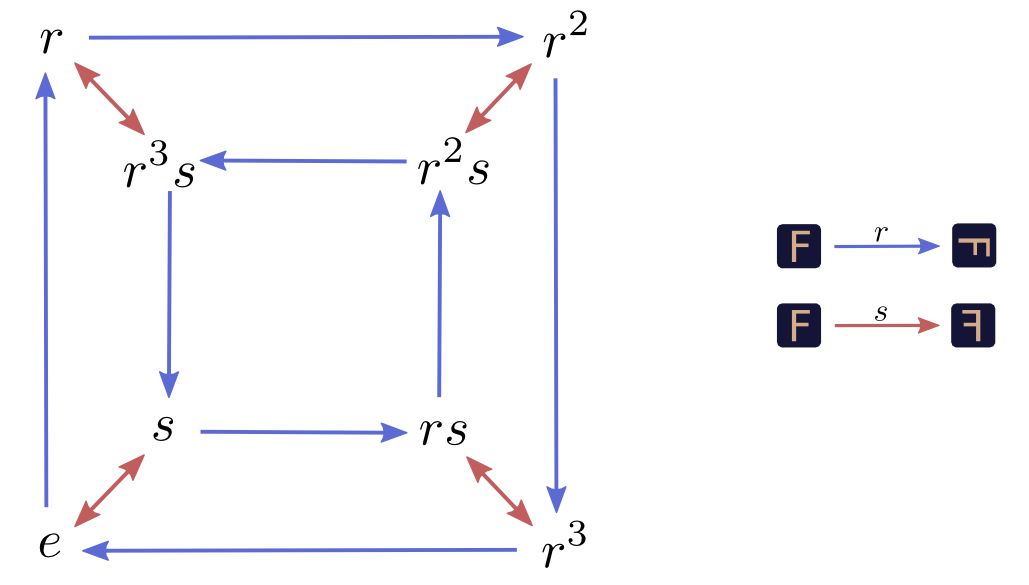
图 3 Cayley关系图3
图3便可被看为一个群。图中的每一个位置,如e、s、r、rs等可看为群中集合的元素,每一种变换是一个元素。将这些元素收集起来便得到了一个变换的集合。
在介绍群的定义之后,对群卷积的概念进行说明。假设我们有三张牌,以变换牌的顺序作为元素定义一个群如图4:
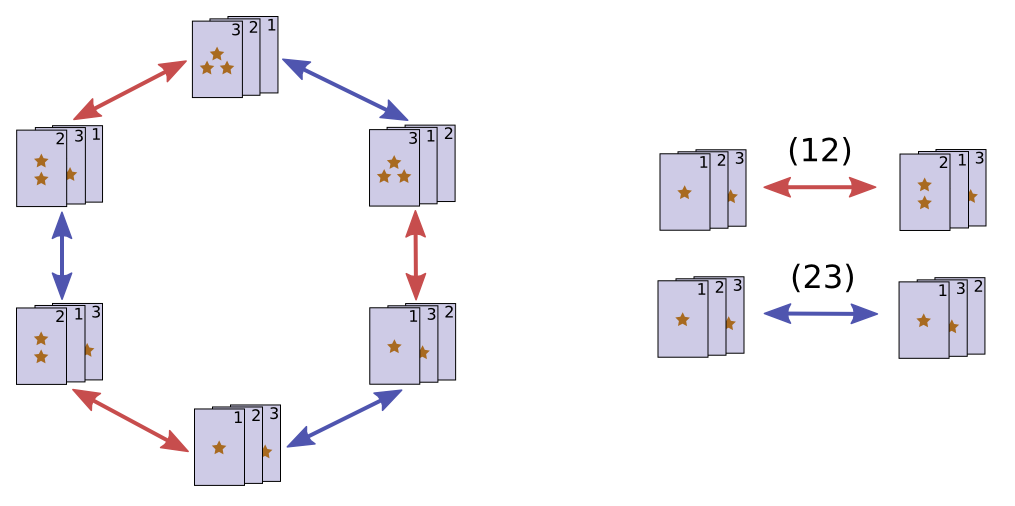
图 4 对称群示意图
现在进行随机洗牌,每一轮洗牌40%的时间进行(12)顺序交换,60%的时间进行(23)顺序交换。第一轮洗牌结束时,三种牌的排序顺序为a,接着进行第二轮洗牌得到排列b。随机洗牌三轮后,三张牌的排列顺序变为c,则排列c出现的概率为:

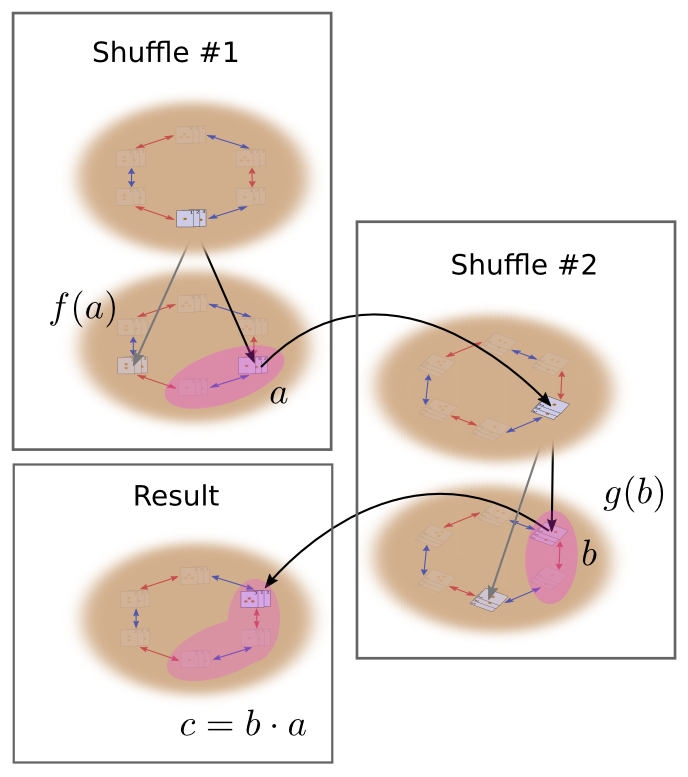
图 5 三轮洗牌流程图
令b=ca-1,则有

再令a=b-1c,可得到:
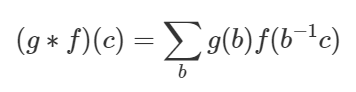
根据卷积的定义,上式即可被看为一种群卷积。
参考文献
[1] https://en.wikipedia.org/wiki/Group_(mathematics)
[2] Carter N. Visual group theory[M]. MAA, 2009.
[3]https://colah.github.io/posts/2014-12-Groups-Convolution/



