定义
使用多个高斯分布的组合刻画数据分布的方法。
高斯分布是一种在自然界大量的存在的、最为常见的分布形式。高斯分布的概率密度为:
其中包含两个参数，μ表示均值，σ为标准差。均值对应正态分布的中心位置，标准差衡量了数据围绕均值分散的程度。
而混合高斯模型（Gaussian Mixture Model，GMM）是对高斯模型进行简单的扩展，GMM使用多个高斯分布的组合来刻画一般的数据分布。从中心极限定理可以看出，高斯分布这个假设其实是比较合理的。其实，不管假设数据服从什么分布，只要有足够多的分布，这个混合模型就会变得足够复杂，就可以用来逼近任意连续的概率密度分布。只是因为高斯函数具有良好的计算性能，被GMM广泛地应用。
GMM的概率密度函数与高斯分布的非常相似，细节上有几点差异。首先分布概率是K个高斯分布的和，每个高斯分布有属于自己的μ和 σ参数，以及对应的权重参数φ，权重值必须为正数，所有权重的和必须等于1，以确保公式给出数值是合理的概率密度值。
求解GMM的过程称为期望最大化算法（Expectation Maximization，EM），它以极大似然估计为基础。如果某个样本已知服从高斯分布，而且通过采样得到了样本数据，极大似然估计可求解这个高斯分布的参数。而在GMM中，要求解的是一个混合模型，只知道混合模型中各个类的分布模型和对应的采样数据，而不知道这些采样数据分别来源于哪一类。
EM算法通过迭代的方式，对数据所属的类别初始化，并不断向真实方向靠近。第一步称为E-step，先对样本做一个最有可能的划分，也就是最大化数据点由各高斯模型生成的概率。
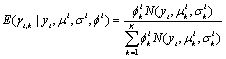
为所属高斯模型的估计，N表示高斯概率密度。这里假设μ和 σ都是已知的，它们的值来自于初始值或者上一次迭代。
第二步称为M-step，有了对所属分布的估计之后，由于每个分布都是一个标准的高斯分布，也有对应的数据点，可以很容易分布求出最大似然所对应的参数值。
，
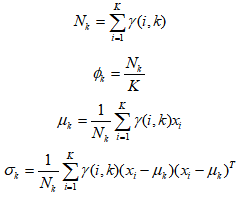
和
表示当前迭代次数时第k个类的权重、均值和方差。
参考文献
[1] https://blog.csdn.net/lin_limin/article/details/81048411
[2] https://github.com/endymecy/spark-ml-source-analysis/blob/master/%E8%81%9A%E7%B1%BB/gaussian-mixture/gaussian-mixture.md
参阅：混合模型、K-均值聚类、高斯分布
