定义
t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法,由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出[1]。t-SNE 作为一种非线性降维算法,非常适用于高维数据降维到2维或者3维,便于进行可视化。t分布是指降维后度量数据点之间距离分布的模型假设,随机一词则更多体现的是该算法由计算机来驱动,通过随机初始化、搬移点来找到最优解的过程。

图 1 通过t-SNE对高维数据降维到2维
思想
t-SNE的思想来自于SNE。SNE是一种非线性降维方法,以一个二维数据的降维为例,假设现在有一个二维数据,需要找到一个最佳的一维流形,把数据嵌入到该流形结构上后,每个点和周围邻居的关系仍然能够保持。何为“最佳的”一维流形?在SNE里面给出了规则:我们任意选取原始数据上的一个点,这个点和其他每个点的距离可以通过正态分布并归一化映射成为概率,换句话说,原始数据中每个点和其他任何点的距离都可以通过一个正态分布来刻画,那么“最佳的”一维流形就是,投影后仍然能够最大程度保持这种分布。
通过上面我的表述可以容易看出,我们的目标就是找出一个低维流形,使任何一个点对其他点的距离分布p和高维上的分布q尽可能接近,那么这是一个优化问题,优化目标(损失函数)就是两个分布的距离,也就是经常提到的Kullback-Leibler Divergence,即K-L散度。K-L散度是通过相对熵的概念来计算分布的差异的,我们知道每个分布都可以通过信息熵计算其携带的信息量,两个分布如果携带的信息量很接近,那么两个信息熵的差会很低,我们就称这两个分布在K-L散度下“距离”很近。
t分布的意义
t-SNE和SNE的主要区别是前面的“t”,即 t Distribution SNE。前面提到了我们试图通过度量低维和高维上距离分布的差异来寻找最佳流形,这里的分布在SNE里都是通过高斯分布来进行拟合。在t-SNE里面是在高维使用高斯分布,但在低维使用t分布,因为对比t分布中间比高斯分布矮,周围比高斯分布高,为了使t分布和高斯分布取得同样的概率,离任意一点很近的点在低维度上会更近一些,离得远的点则在低维会更远,这样可以解决拥挤问题,也就是降维后簇与簇离得很近、难以区分开的问题。
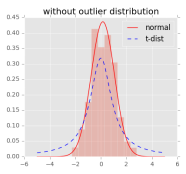
图 2 高斯分布和t分布的对比,可见取得同样概率时,t分布的距离更近
t-SNE的优缺点
优点是,通过t-SNE降维后,数据可以最大限度地成簇并分开。当前的算法很成熟,速度并不像很多文章说的很慢。
缺点如下[2]:
(1)t-SNE对超参的设置比较敏感,设置不当则会导致结果很难看。
(2)t-SNE后簇的大小没有实际意义,与高维分布上的区别可以很大。
(3)t-SNE后簇间距离没有实际意义,与高维分布上的区别可以很大。
(4)t-SNE后聚类出现的不规律形状也没有实际意义。
(5)t-SNE能把随机噪音处理得不像随机噪音,表明结果本身具有一定欺骗性。
参考文献
[1] Laurens V D M , Hinton G . Visualizing Data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(2605):2579-2605.
[2] Distill. How to Use t-SNE Effectively. https://distill.pub/2016/misread-tsne/



