定义
弹性重建算法通过求解反问题从扫描仪采集的波形图像得到描绘组织硬度的定量图像，即弹性图。
磁共振弹性成像的另一关键技术是弹性系数重建算法，在采集完成后，扫描仪自动处理波形图像，以生成描绘组织硬度的定量图像，即弹性图。这些定量图像通常以千帕（kPa）为单位描绘剪切刚度，并且可以以灰度或伪彩图显示[1,2]（图1）。
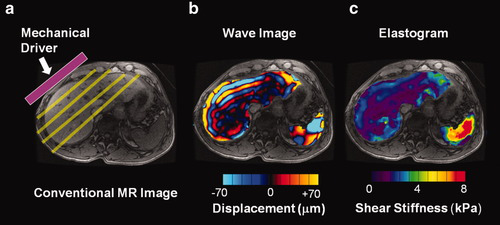
图1 健康志愿者肝脏的扫描示意图(a)，用MRE序列获得的相位图像(b)和重建后的弹性图(c)
根据弹性力学理论，对于微小形变的连续均质各向同性介质，忽略外重力的情况下，只考虑剪切弹性时，弹性系数由外加周期剪切波的频率与剪切波在介质中传播波长来决定.在外加剪切波频率已知时，只要能确定剪切波在介质中传播的波长分布，即可得到介质的弹性系数分布图[3]。
目前常见算法主要为局部频率估算法(Local frequency estimation, LFE)。LFE算法实质是基于不同局域频率(波长倒数)的信号经两个或多个不同滤波器滤波后输出信号的微小差异来进行局部频率计算。原始信号经过两个不同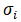
滤波以后的输出信号分别记作O1和O2，其中：
式中，S(x)为原始信号， γlocal 是局部空间频率。将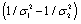
记做D，当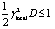
时，上式可以简化为：
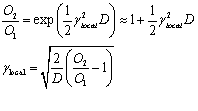
式中表明，信号的局域频率与该信号经不同滤波器后输出的局域信号幅值差异之间的关系，基于此可以确定某一时间信号的局部频率。由局部频率可以求得局部波长，即可得到弹性系统u的分布。
参考文献
[1] Manduca, A, Lake, D, Kruse, S, Ehman, R. Spatio‐temporal directional filtering for improved inversion of MR elastography images. Med Image Anal 2003; 7: 465– 473.
[2] Venkatesh S K, Yin M, Ehman R L. Magnetic resonance elastography of liver: technique, analysis, and clinical applications[J]. Journal of magnetic resonance imaging, 2013, 37(3): 544-555.
[3] 汪红志, 蔡筱云, 王鹤, et al. 基于双带宽高斯滤波器的磁共振弹性图局域频率估算算法研究与实现[J]. 物理学报, 2011, 60(9).
