SIS模型为易感-传染-易感模型，它将人群划分为两类，分别为易感人群（S）和染病人群（I）。模型中认为，染病人群是传染病的传染源，它本身有概率u被治愈成为易感人群，同时也能通过概率λ将传染病传给易感人群，而易感人群被感染后又成为新的传染源。在t时刻，用s(t)代表易感人群在群体中的密度，i(t)表示染病人群在群体中的密度，则SIS模型可以描述为：
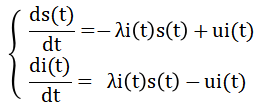
令第二项染病人群的传播等式的右端为0并考虑s(t)+i(t)=1,可以得到方程的两个平衡点(s,i)=(1,0)或(uλ-1, 1-uλ-1)，说明方程中存在一个阈值λc，当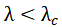
时传染病无法大规模传播，当
传染病会出现大范围的全局传播。
参考文献
[1] https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology#The_SIS_model
