文章名称:Ultrasonic super-oscillation wave-packets with an acoustic meta-lens
发表期刊:Nature Communications
发表日期:2019年7月
1 摘要
薛定谔方程是描述量子力学系统波函数的基本方程,薛定谔方程和傍轴波动方程之间的相似形式允许从量子力学到经典领域的范式转换,从而打开了包括光学超振荡行为在内的大量有趣现象。在这里,我们提出了一种声学超透镜,用于产生不同空间动量的超振荡声波波包,然后将它们叠加到未达到衍射极限的焦点上,直观地表示为微小粒子的环形捕获。此外,基于聚焦的超振荡包,我们通过实验验证了超分辨率超声成像的可能性,为先进的声成像、生物医学应用和多功能远场超声控制开辟了超声超振荡的领域。
2 背景
从理论物理学到应用科学,在各种教科书中都普遍看到了包含频率低于最大限度的波函数,人们凭直觉可能认为限频波函数的变化不会快于其最高频率分量。然而,在1990年代,Aharonov、Berry等人给出了反例,以显示某些波函数的存在,该波函数在比其最高傅立叶分量大得多的频率处短暂振荡,称之为超振荡现象。此后,超振荡现象被引入经典波理论中,这产生了各种不同寻常的影响,例如远场超分辨率聚焦。在过去的几十年中,超越成像衍射极限是光学和声学领域的一个长期目标。自从负折射率和双曲折射率超材料提出以来,已经揭示了携带超分辨率信息的倏逝波会在这些新型材料中被重新采集到。但是由于较大的介质损耗,超分辨率聚焦和成像仅在近场中实现,因此将光或声音聚焦到远场中的深亚波长点具有很大的价值。
在这项研究中,我们利用超振荡波包来克服超声波在远场中的衍射极限。我们直接根据波动方程构造具有时间周期特性的声学超振荡函数,然后展示了一种通过自由优化方式组合超声波的不同空间频率以产生超振荡波函数的静态空间分布的方法。在超声超振荡的演示中,我们设计了厚度约为0.13λ的超透镜,以投影在远场焦区产生衍射极限所需的空间频率分量。产生的超振动包的特点是振幅相对较弱,但压力梯度明显,确保了较大的声辐射力。这种作用力效应是从微粒子的环状捕获实验中观察到的,它显示了光斑的轮廓。此外,基于聚焦的超振荡包,我们通过实验演示了亚波长透镜的超分辨超声成像。
3 原理
图1显示了构造的波函数在不同时间的演变行为。在图1a中,波函数是初始时间t=0的带限函数。当时间在t=1.32π+3πM附近变化时,超振荡发生,其中M是整数,3π是它的周期。图1b清楚地显示了一维情况下的周期性。图1c显示了在t=1.32π附近设计的超振荡时区的演变细节,其中在x=0附近出现非常快的振荡。为了定量评估所构造的超振荡,我们在图1d中绘制了波函数的实部和虚部。我们的结果表明,波函数的两个部分都比其最大频率振荡得更快。在补充视频1中,我们展示了构造的波函数在t=0~1.39π的时间范围内的动态演化。
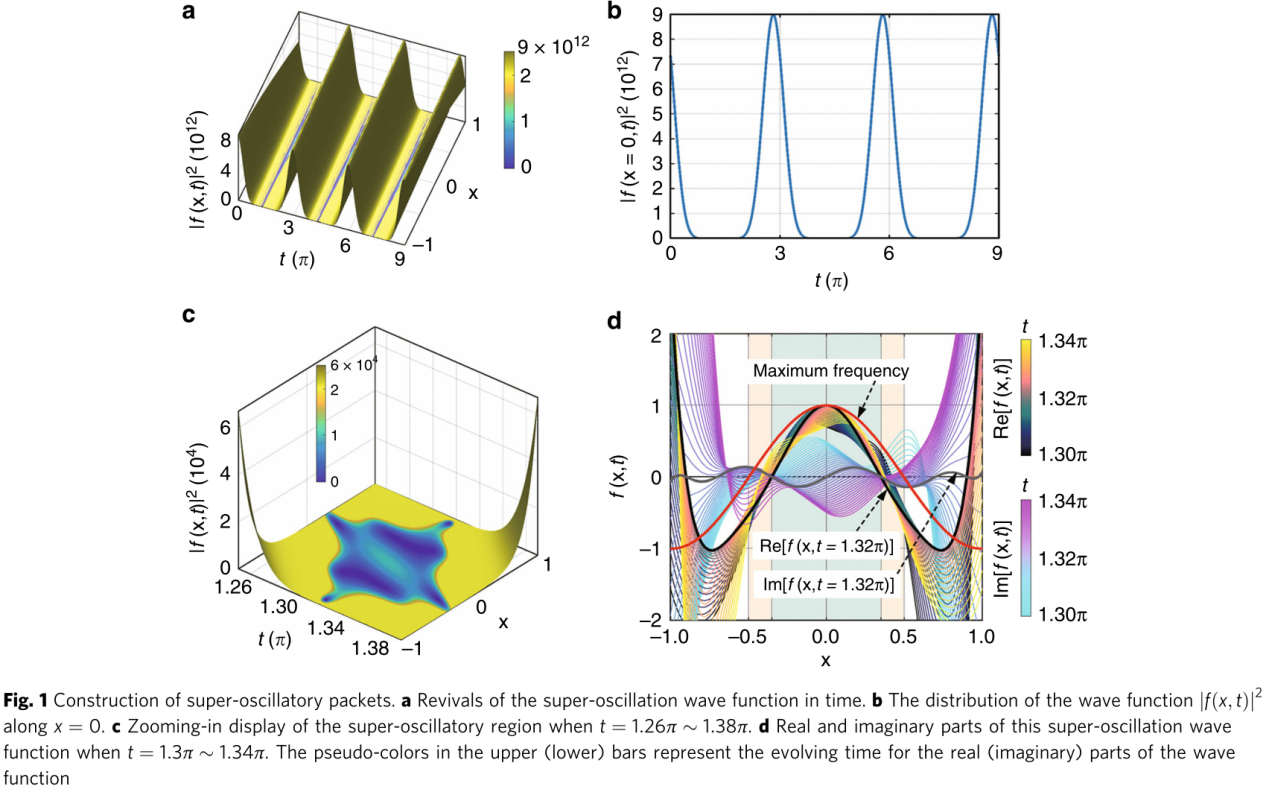
图 1 超振荡波的构造
为了验证声学超振荡,我们设计了一种优化后的超透镜,它建立了超振荡函数的时间频率与超声空间频率之间的映射关系,图2a显示了制造的样品。对于单带菲涅耳波带片,如图2b所示,衍射极限为RD = 0.38λ。为了突破受限区域的衍射极限(-λ/2,λ/2),如图2c所示,需要利用超振荡原理。在z = 5.2λ平面上,我们设计了一个超出衍射极限(< 0.38λ)的主瓣半径为0.3λ的超振荡焦斑。在图2d中,彩色曲线显示了不同空间频率分量的归一化超声强度分布,而由所有分量的精细组合合成的黑色曲线具有超振荡特征。

图 2 超振荡声学超透镜
图3a、b分别显示了x-z平面上的模拟和测量的强度分布。结果表明,在z = 5.2λ处存在一个超振荡场。图3c、d分别表示在z = 5.2λ时x-y平面上的视场(2λ × 2λ)中的模拟和测量的强度分布。在x-y平面视场外,声能约占模拟总能量的23.7%。在图3e中,我们定量地比较了沿着x = (-λ,λ),y = 0,z = 5.2λ模拟和测量的场强,如分别由的黑色实线和带有误差率的蓝色圆圈所示。可以清楚地看到,测量数据与图3中的模拟结果吻合得很好。然而,记录到的半径为约0.3λ的焦斑为我们提供了依据,即根据0.3λ < λD = 0.38λ的超振荡判据,在远场产生了超振荡超声场。这种超振荡效应也可以从计算的局域波数中反映出来,该局域波数远大于零烈度位置的最大空间频率分量。

图 3 声学超透镜的超振动包
4 实验
利用超振荡数据包,我们进一步演示了在水中超透镜的超分辨率超声成像。在实验中,将具有特定图案平面物体放置在超振荡元透镜的焦平面(x-y)中,由三维精密移动台进行位置移动。在测量中,水听器和超透镜是固定的,我们使用蚀刻有0.9 mm直径孔的薄金属板来过滤超振荡场中的旁瓣影响。为了演示超分辨率超声成像,我们通过分子刻蚀技术在0.2 mm厚的钢板上制作了具有亚波长特征的三个图案,如图4a所示。
我们首先演示双缝的超分辨率成像,其中缝宽度和双缝之间的间隙为0.4 mm,间隙大小比瑞利极限小得多。从图4b中可以看出通过我们设计的超振荡超透镜很好地解决了这一差距。但是,使用周期性带状菲涅耳波带片时,成像间隙难以分辨。在图4b中,跨双狭缝中心的强度分布的定量比较为我们提供了成像分辨率显着提高的证据,其中间隙区域对应于强度线(红色曲线)的中心倾斜。然后,为了演示超振动超透镜在对复杂物体成像时的性能,我们使用了卷曲缝隙的图案,缝隙和缝隙的宽度也是0.4 mm。比较图4c,d中的图像,我们发现在区分亚波长特征(即盘绕的缝隙和缝隙)时,超透镜的性能优于周期性带菲涅耳波带片。最后,我们对孔阵列进行成像,以检查该技术可以分辨出多小的孔。最小孔的直径为0.4 mm。图4e,f展示了成像结果。在图4f中,孔是模糊的,最小的孔不能通过周期性带状菲涅耳波带片分辨。我们几乎无法分辨直径约1.2 mm的较大孔。相反,超振荡元透镜所拍摄的图像令人印象深刻,所有主要特征都清晰且可分辨,如图4e所示。
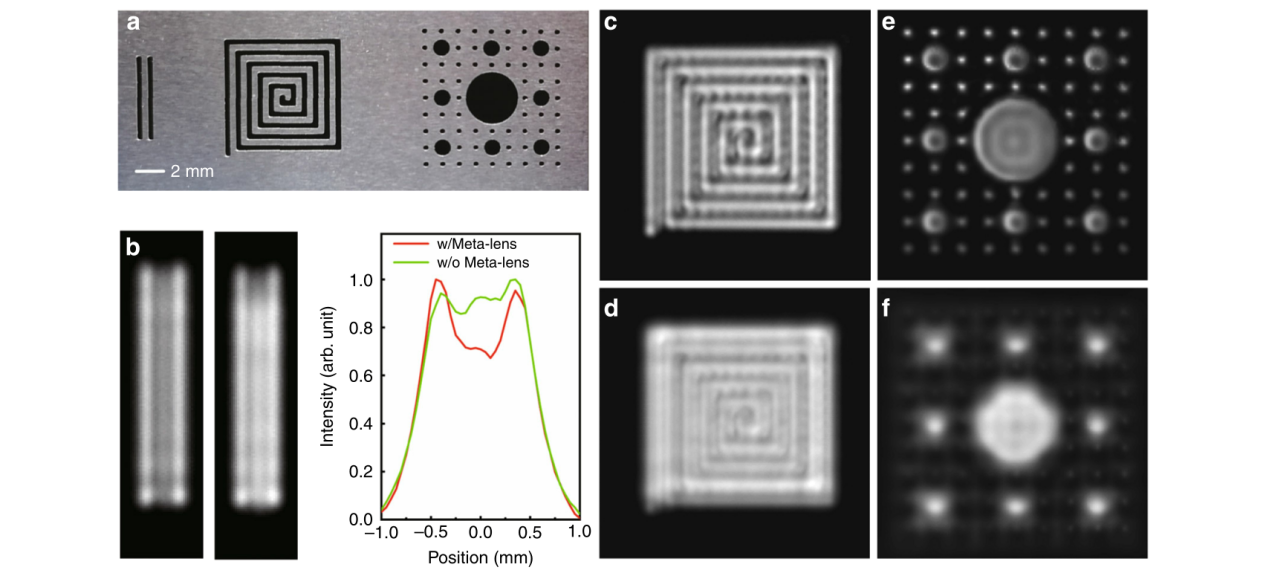
图 4 超分辨率超声成像
5 小结
在这项工作中,我们研究了超声超透镜中的超振动数据包,以超过其最高傅立叶分量的频率对超声整形。我们设计了一个超透镜,该透镜可以投射不同的空间频率分量,以在远场中生成超振动数据包。利用优化后的超透镜,可以观察到超振荡超声包打破了远场中的瑞利衍射极限。进一步显示了具有亚波长特征的各种复杂图案的超分辨率成像结果。这项工作开创了超声领域的新局面。超振荡技术使我们能够灵活地控制超声,使其超出远场的衍射极限,这可能会对改变超声治疗和成像领域有重大影响。
参考文献
Shen YX, Peng YG, Cai F, et al. Ultrasonic super-oscillation wave-packets with an acoustic meta-lens. Nat Commun. 2019;10(1):3411.



