定义
基于Snake模型的改进变分图像分割方法。
Snake模型作为一种早期经典的变分图像分割方法，每一项都有独特的含义。然而，这些约束条件过于强烈，而且曲线是用参数方程的形式表示的，一个方程只能表示一条闭合的曲线，无法同时表示分裂后的多条曲线。另外参数方程不一样得出的解也有可能不一样。也就是说Snake模型其实只能提取一个物体的边界，这个边界必须是光滑的，而且分割结果和初始曲线的形状有很大关系。
Caselles等人将Snake模型减少约束后得到了新的能量方程：
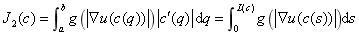
J2(c)的积分限为曲线c的长度L(c)，与c的参数化形式无关了，只与曲线的几何形状有关。一条曲线的长度L可以用对弧长的曲线积分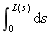
表示，因此方程J2(c)可以看成一个加权的曲线长度，权重是
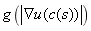，函数g如之前所说是物体轮廓线，它蕴含了物体边界的信息。这个模型称为测地主动轮廓模型（GAC）。测地线是指在曲面上两点间的最小距离路径，而这里是基于图像边界内容，搜索与物体边界相近的最短曲线。
使用梯度下降法解这个泛函，对应的微分方程为：
为曲线上每一点的曲率，N为曲线上每一点的法线方向。整个推导过程从梯度下降的方向出发，使得曲线的曲率下降，既有缩短曲线的效果，也有平滑曲线的效果。也就是去掉Snake的平滑项是合理的，其余部分仍能使得曲线曲率最小化。
参考文献
[1] Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models[J]. International journal of computer vision, 1988, 1(4): 321-331.
[2] Caselles V, Catté F, Coll T, et al. A geometric model for active contours in image processing[J]. Numerische mathematik, 1993, 66(1): 1-31.
参阅：变分法、Snake模型、水平集
