定义
一种基于区域的变分图像分割检测算法。
变分图像分割按照曲线演化方式,可以分为两大类,一类是基于边缘的变分图像分割方法,如Snake模型,从目标物体的内部或外部演化曲线,逐渐向目标物体的边缘靠拢。另一类则是基于区域的变分图像分割方法,以Mumford-Shah(M-S)模型为代表,找到图像的一个分片光滑的近似,和去噪有些类似,如下图所示,左图是原始图像,右图为分割结果。

Mumford和Shah在1989年提出了上面这个问题,构造了M-S模型。这个模型是基于相似的区域来分割图像的,是最早的一个基于区域的主动轮廓模型。假设u0是初始图像,我们需要寻找一组图像 ,其中u是u0的“简化版”,K是分割出的边界的集合。构造这样一个能量泛函:
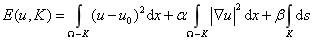
其中Ω是图像域,α和β都是控制权重的常数,![]() 是轮廓集合K的长度。
是轮廓集合K的长度。
对于目标图像u,这个泛函要做出这样几项约束:最小化第一项表明u-u0越小越好,表示这个简化后的u和原图像要尽可能接近;最小化第二项表明目标图像u的梯度越小越好,表示这个“简化版”的图像要尽可能由光滑的同质区域组成,边缘少,梯度小;最小化第三项表明分割出的边界K越短越好,分割结果要尽可能简洁。
同时保持能量泛函E(u,k)中的三项会非常难以求解,它包括两个变量:重建图像与边界集合。在这些基于区域的分割方法中,一个经典的改进方法是Ambrosio等人提出的一个近似方程。在这个方程里,模型中的边界集合用一个可以表示边缘的连续函数代替,也就是寻找一个泛函序列 来逼近 ,避免了对泛函E直接离散化求解。
下图为使用这种近似方法的分割结果,展示了初始的网格线一步步演化到灰度值相近区域边缘的全过程。

基于区域的主动轮廓模型的演化过程
参考文献
[1] Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on pure and applied mathematics, 1989, 42(5): 577-685.
[2] Ambrosio L, Tortorelli V M. Approximation of functional depending on jumps by elliptic functional via t‐convergence[J]. Communications on Pure and Applied Mathematics, 1990, 43(8): 999-1036.
参阅:变分法、Snake模型



