定义
Hammersley-Clifford 定理证明了马尔可夫随机场本身就是吉布斯随机场,马尔科夫随机场的概率分布一定可以表示成一系列非负函数乘积形式。定理之所以成立,是因为马尔科夫场的平滑假设,即“一个像素要和周围像素存在关系,即他们的灰度尽可能相近,与较远的像素无关”。定理更为严谨的描述是,下列两个定义等价[1]:
1、一个无向图模型G称之为马尔科夫随机场(MRF),如果两个顶点被观测顶点分割情况下条件独立。也就是说对图中任意顶点Xi,以下条件属性成立:
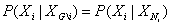
XG\i代表除了Xi 之外的所有顶点,XNi代表所有与Xi 相连的顶点。
2、在无向图模型G上的一个概率分布P(X) 称之为吉布斯分布,如果它能够因子分解为定义在团(clique)上的正函数的乘积,这些团覆盖了G的所有顶点和边。即:

CG是G上所有最大团的集合, 是归一化常量。
是归一化常量。
意义
该定理是使用马尔科夫场进行图像去噪的基础。马尔科夫场进行图像去噪,是将图像假设为一个马尔科夫随机场,然后基于先验假设(马尔科夫场的局部平滑特性)求解其概率最高的状态。计算方法是通过不断抽样出新的样本,样本的概率通过最大后验估计(MAP)将后验概率被转化成极大似然项和先验概率进行估计,从而不断迭代寻找概率最高的状态。
在去噪问题中,我们规定了一个先验知识:去噪的图像是一个马尔可夫随机场。由于H-C定理指出了其与吉布斯分布的等效性,那么我们最大化先验知识的概率,就被转化成了最小化能量,从而将一个样本图像的概率通过各个小区域的能量的乘积表示,表示方法可以参照Ising模型,思想就是一个图像区域内各个像素的亮度变化方向一致,则能量更低,这里不作详细阐述。其次,H-C定理指明了优化的方向:能量越小,概率越大,这个思想是从统计热力学的证明过来的,该证明过程表明了通过能量的负指数表达概率的合理性。
参考文献
[1] Proof of Hammersley-Clifford Theorem, February 3, 2008, Samson Cheung. Link.



