解决的问题
如何利用计算机进行高维分布的采样,在求解复杂积分等方面有重要应用。采样求解数学问题的核心思想就是通过频率来逼近概率,举例而言,想要求解下图所示的不规则图形的面积,可以通过无限次撒豆子(从均匀分布中采样作为x、y坐标),统计落在图形内、矩形内的豆子比例,就可以求解出相应面积。
1953年,为了研究粒子系统的平稳性质,Metropolis考虑了物理学中常见的波尔兹曼分布的采样问题,首次提出了基于马氏链的蒙特卡罗方法(Metropolis算法),之后由Hastings 对其加以推广[1]。
核心思想
1、马尔科夫链的收敛特性
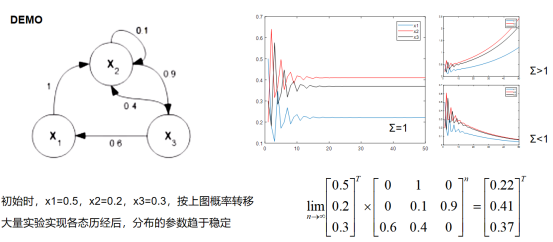
上述例子可以看到,给定一个初始状态,给定一个按特定概率转移的方式,在经过大概20次转移后,最终x1~x3的取值趋于稳定。事实上,这个稳定状态只取决于转移矩阵,和初始状态无关。每次转移实际上对应均匀分布的采样,稳态分布则可以被设计成一个复杂分布,那么就可以通过设计转移矩阵,通过均匀分布来逼近复杂分布。注意到这里的转移矩阵任何一行的和为1,表明没有能量泄露,这样才会最终趋于稳定,称为细致平稳条件。
2、M-H采样
从直觉上看,抽样的目的是希望目标分布中概率较大的点应该尽可能多的出现。因此对于计算机均匀采样产生的样本,可以根据目标分布计算获得的概率,进行一定程度的接收或者拒绝,使最终获取到的样本符合目标分布,这就是M-H采样的核心思想,背后的理论是通过设定接受率α,使构造的马尔科夫链符合细致平稳条件,从而逼近目标分布。
条件
(1)先验分布必须已知。
(2)马尔科夫链必须满足细致平稳条件。
缺点与改进
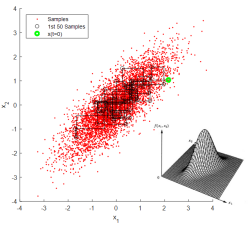
M-H采样的缺点是面对复杂的高维分布时计算量很大,而且极易遇到接受率过低导致大量样本被拒绝、采样效率很低的问题。Gibbs采样巧妙地将转移矩阵设置为条件概率,按照条件概率转移构造马尔科夫链,优点是天然地满足细致平稳条件,而且计算条件概率要比直接计算复杂分布对应的概率要简单的多。Gibbs采样的具体实施方法是在每次采样时先固定其他维度,仅对一个维度进行采样,然后多次、随机选取维度进行迭代,下图展示了对二维高斯分布进行Gibbs采样的过程。
参考文献
[1] 朱新玲. 马尔科夫链蒙特卡罗方法研究综述[J]. 统计与决策, 2009, 000(021):151-153.



