定义
多变量统计领域中的一种分析方法,是使用核方法对主成分分析的非线性扩展,即将原数据通过核映射到再生核希尔伯特空间后再使用原本线性的主成分分析。
Kernel PCA与PCA不同的是,其主要解决线性不可分的问题,如图1所示:
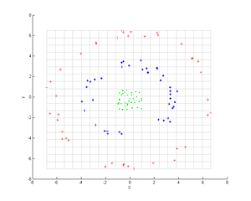
图1 线性不可分问题
PCA的思想是做直线或平面的投影,而圆环没办法在原空间上进行线性划分。因此Kernel PCA就要求我们需要一种变换,将上述线性不可分问题转化为线性可分问题进行处理,这样才能利用PCA的线性可分性质。如图2所示:
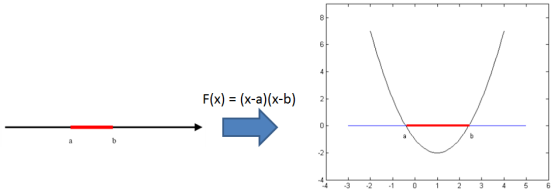
图 2 红黑的线性不可分问题,利用二次函数来隔开
a和b的红色线段,和黑色线原本不能利用一条直线来分开,但转换思路我们可以通过一个二次函数将其分开。

图 3 不同空间的数据分布
我们回到之前的问题,圆环是不是换个空间就线性可分了呢?当然!我们发现原本线性不可分的空间只需要提高其所在空间的维度就可以将线性不可分转化为线性可分,因此其问题核心就在于Kernel的引入可以将数据的空间维度不断提高,其数学解释如下(以高斯核举例):

图 4 高斯核将数据映射到高维甚至无穷维的原理
因此,Kernel PCA实际上就是通过Kernel的升维作用,将线性不可分问题转化为线性可分问题,这样PCA就可以使用了。
参考文献
[1] Schölkopf B, Smola A, Müller K R. Kernel principal component analysis[C]//International conference on artificial neural networks. Springer, Berlin, Heidelberg, 1997: 583-588.
[2] https://blog.csdn.net/baimafujinji/article/details/79376378
参阅:
Kernel PCA、Nonlocal PCA、Robust PCA、Sparse PCA、PCA工具包安装及其使用



