定义
傅里叶变换在物理学和工程学中常用的一种线性积分变换，在1822年由Joseph Fourier提出，他证明了一些函数可以写成无数个正弦函数和余弦函数的和[1]，因此可以实现信号在时域(或空域)和频域之间的变换。根据信号在时域(空域)或频域的特性，可以分为以下几种情况：
- 当信号在时间上为连续非周期时，对应为连续傅里叶变换；
- 当信号在时间上为连续周期时，对应为傅里叶级数；
- 当信号在时间上为离散非周期时，对应为离散时间傅里叶变换；
- 当信号在时间上为离散周期时，对应为离散傅里叶变换；
其中傅里叶级数变换可以定义为：
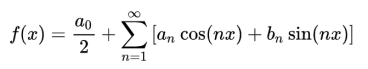
其中，an和bn是实频率分量的振幅。整个过程可以如图1所示：
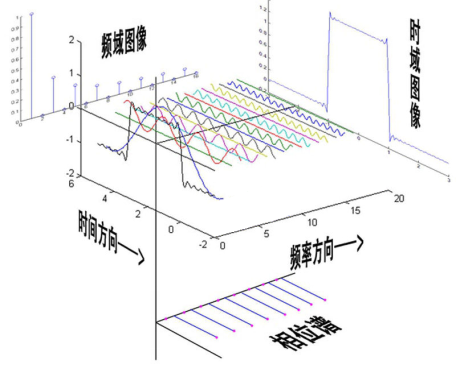
图 1 傅里叶级数变换示意图。
傅里叶变换是对傅里叶级数的扩展，由它表示的函数的周期趋近于无穷。因此一般情况下，若“傅里叶变换”一词不加任何限定语，则指的是“连续傅里叶变换”，其定义式为：
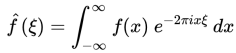
其中，f是一个可积函数，
为任意实数。
傅里叶逆定理
傅里叶逆定理提出f可由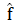
确定，傅里叶在其1822年出版的著作《热分析理论》中首次引入这个定理。虽然现在标准下的证明直到很久以后才出现。f和 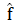常常被称为傅里叶积分对或傅里叶变换对。表2为常见的傅里叶变换对。
图表 2 常见傅里叶变换对
参考文献
[1] Fourier, J.B. Joseph (1822), Théorie analytique de la chaleur (in French), Paris: Firmin Didot, père et fils, OCLC 2688081.
参阅：正交变换、拉普拉斯变换
