定义
光束的电场振荡方向。
在许多方面,光可以被描述为一种波现象(→波光学)。 更具体地说,光波被认为是电磁横波,即具有电场和磁场的横向振荡。
线性极化
极化方向与电振荡有关,而不是磁性振荡。
在最简单的情况下,光束是线性偏振的,这意味着电场在垂直于光束轴的某个线性方向上振荡,磁场在垂直于传播轴和电场方向的方向上振荡。 极化方向取为电场振荡的方向(即,不是磁场振荡的方向)。 例如,在z方向上传播的激光束可能在垂直(y)方向上具有电场振荡,在水平(x)方向上具有磁场振荡(见图1);它可以称为垂直极化或Y极化。 从另一个角度来看,图 2 的第二部分也显示了这一点。
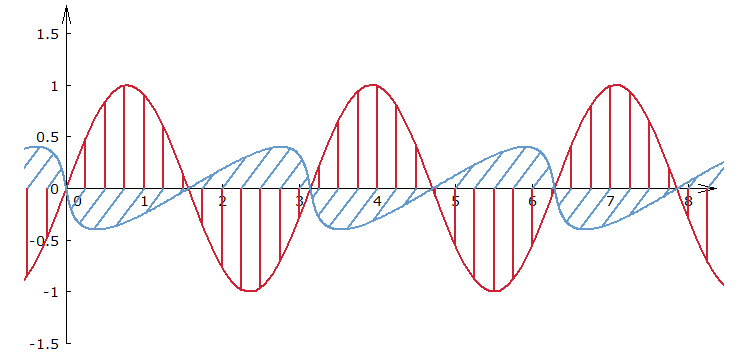
图1:从左到右传播的电磁波。电场(红色)在垂直方向上振荡,磁场(蓝色)在垂直于绘图平面的方向上振荡。
当然,偏振可以具有垂直于光束轴的任何其他方向。 请注意,极化旋转180°不会导致物理上不同的状态。
圆极化和椭圆极化
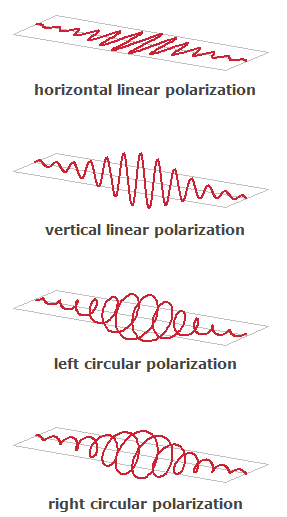
图2:激光发射的不同偏振状态,图示了从左到右传播的几个周期脉冲。
圆极化状态可以在数学上获得为垂直和水平方向上电场振荡的叠加,两者强度相同,但相对相变为90°。 实际上,这导致电场矢量的快速旋转 - 每个光学周期一次 - 保持恒定的幅度。
一种区分左圆极化和右圆极化(见图2)。 例如,左圆极化意味着电场(和磁)矢量沿传播方向旋转。 对于逆向光束观察的观察者来说,旋转当然具有相反的方向。
如果水平和垂直电场矢量的振荡不具有相同的强度,则具有椭圆极化的情况,其中投射到垂直于传播方向的平面的电场矢量沿椭圆移动。
波片的影响
光的偏振状态通常使用不同类型的光波片来操纵。 一些例子:
- 使用半波片(λ/2板),可以将线性偏振态旋转到任何其他方向。
- 对于四分之一波片(λ/4板),其轴与偏振方向成45°,可以将线性偏振状态转换为圆形(反之亦然)。
- 通过一个半波片和两个四分之一波片的组合,可以实现偏振控制器,通过它可以通过正确旋转三个板来进行任意偏振转换。
真偏振旋转
如上所述,波片或其它双折射光学元件可以旋转线性偏振的方向,但更一般地在这种元件之后将获得椭圆偏振状态。 真偏振旋转,其中始终保持线性偏振状态(只是方向可变),可以以光学活动的形式发生。 一些光学活性物质,如普通糖(蔗糖)可以在例如几毫米的传播长度内产生大量的旋转角度。 光学活性可以用旋光仪精确测量。
虽然光学活性通常是由手性分子的存在引起的,两种可能的对映计之间存在浓度差异,但它也可以由非天然光学活性物质中的磁场诱导。 这被称为法拉第效应,在法拉第旋转器和法拉第隔离器中被利用。
径向和方位偏振
在前面的案例中,假设电场矢量的方向在整个光束轮廓上是恒定的。 但是,有些光束并非如此。 例如,存在径向偏振光束,其中光束轮廓上任何点的偏振方向为径向,即远离光束轴。
请注意,径向或方位偏振状态需要零电场强度,因此光束轴上的光强度也消失;例如,它与高斯光束不兼容。 径向偏振光束经常表现出一种甜甜圈轮廓。
径向偏振激光束可以从具有某些光学元件的线偏振光束产生,但也可以直接从激光获得径向偏振发射。 这种方法应用于固态体激光器的优点是可以避免去极化损耗[4]。 此外,还有一些应用受益于径向偏振光。
还有方位偏振光束,其中任何点的电场方向都是切向的,即垂直于通过点和光束轴的线。
p 和 s 极化
当光以某个角度照射到光学表面时,光的偏振状态通常很重要。 当偏振方向位于入射光束和反射光束跨越的平面上时,线性偏振状态表示为p偏振。 方向垂直于该极化的极化称为s极化。 这些指示起源于德国:s = senkrecht = 垂直,p = 平行。
不幸的是,这些术语有时在衍射光栅的上下文中也具有不同的含义[9]。
琼斯微积分
单色光的偏振状态通常用琼斯矢量描述,如果传播发生在z方向上,则在x和y方向上具有复杂的电场振幅。 琼斯矢量可能在光束上的某个区域是恒定的,或者它可以变化,例如径向偏振光束(见上文)。 波片、偏振器和法拉第旋转器等光学元件的效果可以用琼斯矩阵来描述,琼斯矢量可以通过乘法变换。 (假设输入和输出幅度之间存在线性关系。 这种光学元件的整个序列可以用单个琼斯矩阵来描述,该矩阵是作为对应于组件的矩阵的乘积获得的。
在某些情况下,多色光可以用单个琼斯矢量来描述,因为它的所有频率分量基本上都具有相同的偏振状态。 然而,在其他情况下,极化状态基本上与频率有关。
琼斯矢量只能用于完全定义的偏振状态,不能用于具有随机性质的非偏振或部分偏振光束(见下文)。
非偏振和部分偏振光束
当使用偏振器进行分析时,无论旋转方向如何,每种偏振状态都有 50% 的功率,则光束称为非偏振。 在显微镜下,这通常意味着偏振状态是随机波动的,因此平均没有检测到偏振。 请注意,对于严格的单色光,这种波动是不可能的。
线偏振光可以用偏振扰频器去偏振(制成非偏振),它应用上述随机偏振变化,或至少是准随机变化。
光也有部分偏振状态。 这些可以用斯托克斯向量(但不能用琼斯向量)来描述。 此外,可以定义一个偏振度,该偏振度可以从斯托克斯矢量计算,并且可以在0(非极化)和1(全极化)之间变化。
完全极化态可以与所谓的庞加莱球面上的点相关联。 部分极化态对应于该球体内的点;非偏振光由其中心的点表示。
极化与应用的相关性
光的偏振对于一系列应用都很重要。 一些例子是:
- 仅在光学表面(→布鲁斯特角)的p偏振下获得最小反射损耗的设置)
- 非线性频率转换,其中非线性晶体中的相位匹配通常只在一个偏振方向上获得
- 干涉仪、偏振束组合系统、半导体光放大器、光调制器等偏振相关设备中的激光束加工
偏振消光比
线性偏振的程度通常用偏振消光比(PER)来量化,该比定义为两个偏振方向上的光功率比。 它通常以分贝为单位,并通过记录偏振片的方向相关功率传输来测量。 当然,偏振片本身的消光比必须高于激光束的消光比。
激光束的偏振
在许多情况下,激光的输出是线性偏振的。 不同的机制可以对此负责:
- 激光增益可能与偏振有关。 一些各向异性激光晶体就是这种情况(例如Nd:YVO4或Nd:YLF),也存在于一些半导体光放大器中。
- 谐振器损耗可能与偏振有关,例如,当谐振器包含布鲁斯特板甚至仅包含略微倾斜的光学元件时。
请注意,两个偏振方向的极小增益或损耗差足以获得稳定的线性偏振,前提是激光谐振器内没有明显的偏振模式耦合。
另一方面,激光输出的偏振状态可能会受到干扰,例如随机(和温度相关)双折射,例如在光纤中(如果它们不是保持偏振或单偏振光纤)以及激光晶体或玻璃中由于热效应(→去偏振损耗)而发生). 如果激光增益不依赖于偏振,则双折射的微小漂移可能导致偏振状态的较大变化,并且光束轮廓上的偏振状态也会发生显着变化。
参考文献
[1] V. G. Niziev and A. V. Nesterov, “Influence of beam polarization on laser cutting efficiency”, J. Phys. D 32 (13), 1455 (1999), doi:10.1088/0022-3727/32/13/304
[2] A. V. Nesterov and V. G. Niziev, “Laser beams with axially symmetric polarization”, J. Phys. D 33 (15), 1817 (2000), doi:10.1088/0022-3727/33/15/310
[3] Q. Zhan, and J. Leger, “Focus shaping using cylindrical vector beams”, Opt. Express 10 (7), 324 (2002), doi:10.1364/OE.10.000324
[4] I. Moshe et al., “Production of radially or azimuthally polarized beams in solid-state lasers and the elimination of thermally induced birefringence effects”, Opt. Lett. 28 (10), 807 (2003), doi:10.1364/OL.28.000807
[5] ISO Standard 12005, “Lasers and laser-related equipment – Test methods for laser beam parameters – Polarization”
[6] Q. Zhan, “Cylindrical vector beams: from mathematical concepts to applications”, Advances in Optics and Photonics 1 (1), 1 (2009), doi:10.1364/AOP.1.000001
[7] M. Rumpel et al., “Circular grating waveguide structures for intracavity generation of azimuthal polarization in a thin-disk laser”, Opt. Lett. 37 (10), 1763 (2012), doi:10.1364/OL.37.001763
[8] A. Z. Goldberg et al., “Quantum concepts in optical polarization”, Advances in Optics and Photonics 13 (1), 1 (2021), doi:10.1364/AOP.404175
[9] R. Paschotta, “Conflicting definitions of s and p polarization”, The Photonics Spotlight 2012-03-03



