定义
干涉仪由两个高反射镜组成,形成一个驻波谐振器。
法布里-珀罗干涉仪(也称为法布里-珀罗谐振器)是一种线性光学谐振器(或腔体),由两个高反射镜(具有一些小透射率)组成,通常用作高分辨率光谱仪。 人们利用这样一个事实,即通过这种谐振器的传输表现出尖锐的共振,并且它们之间的共振非常小。
工作原理
以下解释,假设无损对称高精细法布里-珀罗,有助于理解其工作原理:
- 只有当输入波的光频率接近谐振器的谐振频率之一时,谐振器中的大量循环光功率才有可能。
- 在共振中,通过输入镜泄漏的输入波的贡献对循环波进行了建设性的补充。 而且,反射场存在破坏性干扰:输入镜反射的输入场被谐振器泄漏的场抵消。 因此,共振中实际上没有反射。
- 在反共振中,循环场相当弱,大部分辐射在输入镜处反射。 从谐振器泄漏到输入源的弱场对反射场进行了建设性的补充。
图1显示了示例案例中与频率相关的透射率:
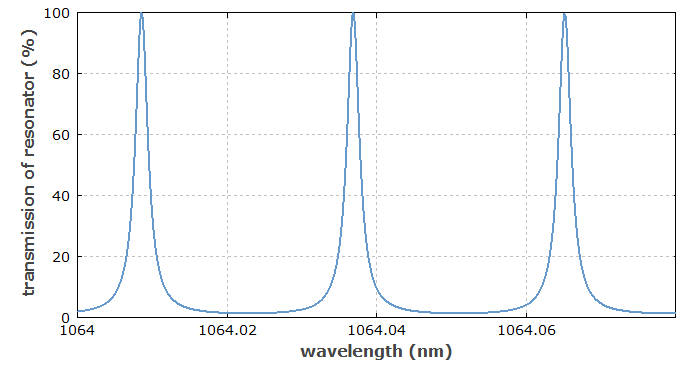
图1:镜面反射率为90%的线性法布里-佩罗腔的频率相关传输。
谐振频率通常可以通过用压电陶瓷促动器改变腔体长度(反射镜距离)来调节。 当施加到压电陶瓷的电压周期性变化时,例如三角形时间形状,并且用光电探测器和示波器监测发射功率与时间的关系,后者可以直接显示入射光的光谱,前提是光谱宽度小于自由光谱范围,并且扫描速度足够慢以达到谐振器的准静止状态。
以下动画图显示了调整居住条件时反射和传输的复振幅如何涉及。
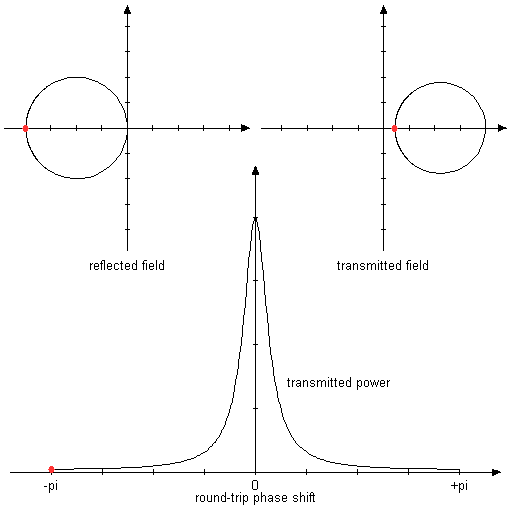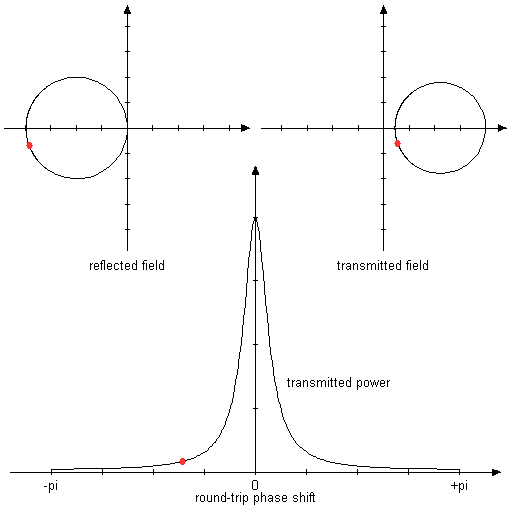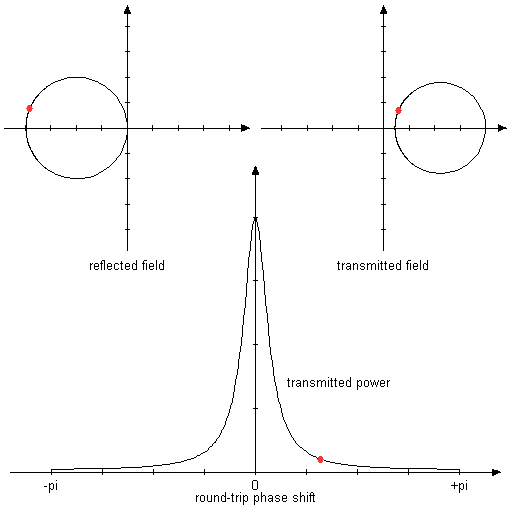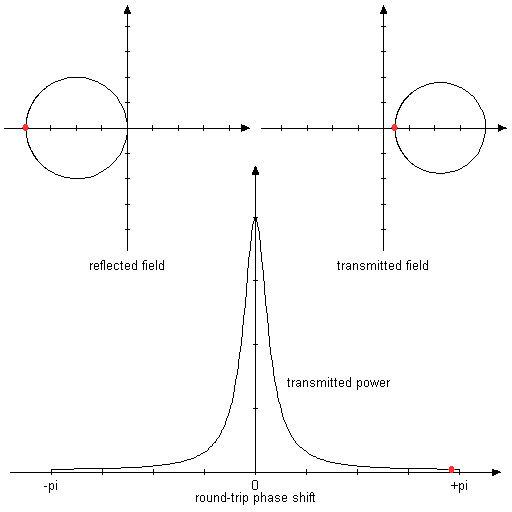
图2:动画图表,显示反射和传输的复振幅以及往返相移变化时的功率传输。 假设两个反射镜的反射率为80%。 在这种对称情况下,共振获得全透射和零反射。
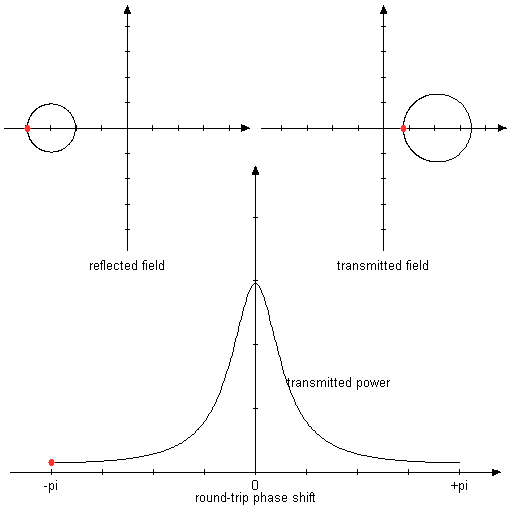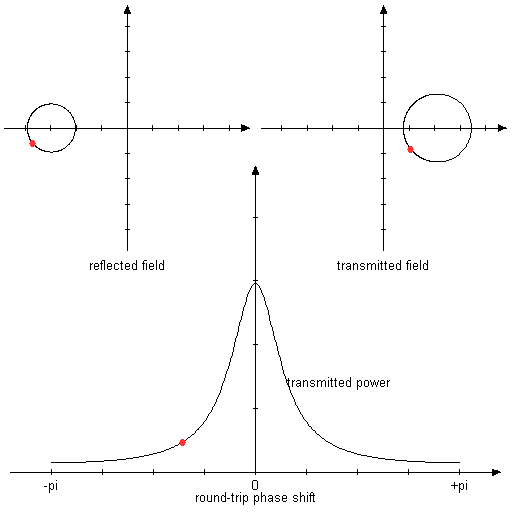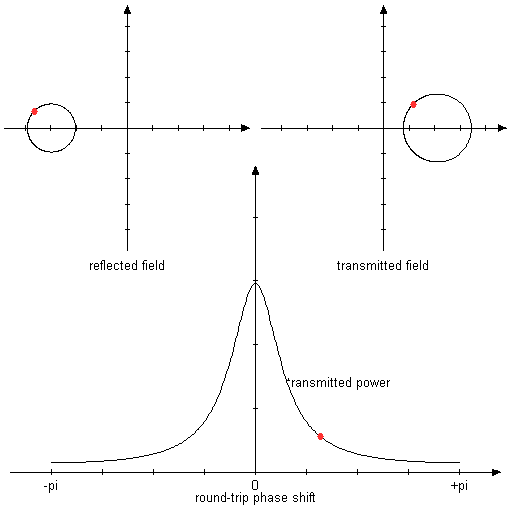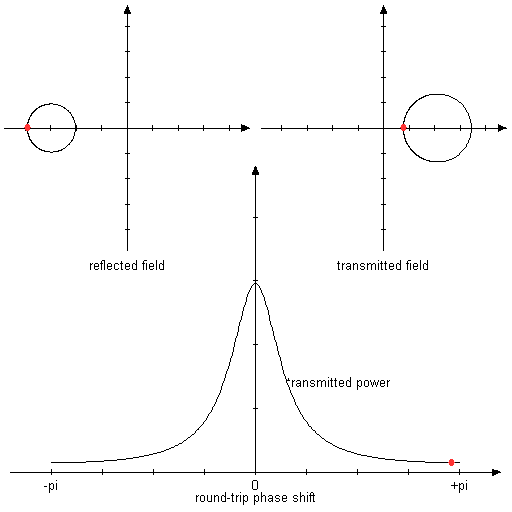
图3:与上述相同,但镜面反射率为80%和50%。 在这种不对称的情况下,反射在共振中不再归零。
变型
严格来说,根据定义,法布里-珀罗干涉仪由两个平面镜组成,但该术语也经常用于带有曲面镜的谐振器。 从理论角度来看,平面-平面光学谐振器的特殊之处在于它们的谐振器模式延伸到镜子的边缘并经历一些衍射损失。 然而,法布里-珀罗干涉仪通常与直径小得多的输入光束一起使用,这些输入光束实际上与谐振器模式并不真正匹配。 对于通常较小的镜间距,往返行程内的衍射较弱,这种偏差不是很重要。
图4:法布里-佩罗干涉仪。
通常,法布里-佩罗干涉仪是在反射镜之间具有自由空间光传播的器件。 但是,该术语有时也用于包含在波导中的设备。 例如,法布里-佩罗激光器是激光二极管,其中包含有源(放大)波导,末端带有某种镜子。
应用
法布里-珀罗干涉仪的典型应用是检查激光器是在单个谐振器模式下还是在多个模式下工作。 高精度法布里-珀罗干涉仪也用作参考腔和光谱分析。
对于光谱分析,法布里-珀罗干涉仪通常做得足够短,以实现足够大的自由光谱范围;共振的带宽是自由光谱范围除以精细度。 由于高反射率,精细度可能很高(远高于1000,超级反射镜甚至更高)。 对于给定的精细度,可以通过增加反射距离来提高波长分辨率,但代价是减小自由光谱范围,即可能进行独特光谱分配的范围。
法布里-珀罗干涉仪的一个变体是Gires-Tournois干涉仪。 这不是用于光谱分析,而是用于产生色散。
参考文献
[1] C. Fabry and A. Pérot, “Théorie et applications d’une nouvelle méthode de spectroscopie interférentielle”, Ann. de Chim. et de Phys. 16 (7), 115 (1899)
[2] J. Stone and D. Marcuse, “Ultrahigh finesse fiber Fabry–Pérot interferometers”, J. Lightwave Technol. 4 (4), 382 (1986), doi:10.1109/JLT.1986.1074739
[3] E. D. Palik, H. Boukari, and R. W. Gammon, “Experimental study of the effect of surface defects on the finesse and contrast of a Fabry-Perot interferometer”, Appl. Opt. 35 (1), 38 (1996), doi:10.1364/AO.35.000038
[4] M. Suter and P. Dietiker, “Calculation of the finesse of an ideal Fabry–Perot resonator”, Appl. Opt. 53 (30), 7004 (2014), doi:10.1364/AO.53.007004
[5] N. Ismail et al., “Fabry-Pérot resonator: spectral line shapes, generic and related Airy distributions, linewidths, finesses, and performance at low or frequency dependent reflectivity”, Opt. Express 24 (15), 16366 (2016), doi:10.1364/OE.24.016366
[6] C Saavedra et al., “Tunable fiber Fabry–Perot cavities with high passive stability”, Opt. Express 29 (2), 974 (2021), doi:10.1364/OE.412273
[7] A. E. Siegman, Lasers, University Science Books, Mill Valley, CA (1986)
[8] J. M. Vaughan, The Fabry-Pérot Interferometer: History, Theory, Practice and Applications, CRC Press (1989)
[9] R. Paschotta, Photonics Spotlight article: The resonator mystery



