定义
一种用于完整表征超短光脉冲的技术。
频域分辨光学开关[1,3]是一种用于“完整”表征超短脉冲的技术,即不仅用于测量脉冲能量或脉冲持续时间等脉冲参数,还用于测量全时间依赖电场(包括光相)或(等效)光谱,包括频率相关光谱相位。 (无法测量载波包络偏移和脉冲到达时间。) 这项技术是由佐治亚理工学院的Rick Trebino研究小组开创的。
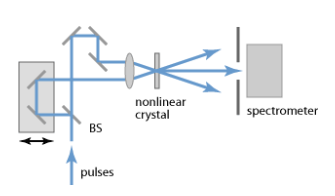
图1:SHG FROG形式的频率分辨光学门控设置。两个光束的非线性混合积的频谱作为相对时间延迟的函数进行测量。
FROG测量的典型设置(图1)与强度自相关器类似,不同之处是用光谱仪(通常是摄谱仪)取代光电探测器,必须对其进行校准才能获得正确的光谱形状。 FROG测量涉及记录数十或数百个光谱,用于两个脉冲到达时间差的不同设置。 这些数据可以用所谓的FROG迹线的形式说明(见图2),这是一种频谱图,用色标显示强度作为时间延迟和光学频率(或波长)的函数。
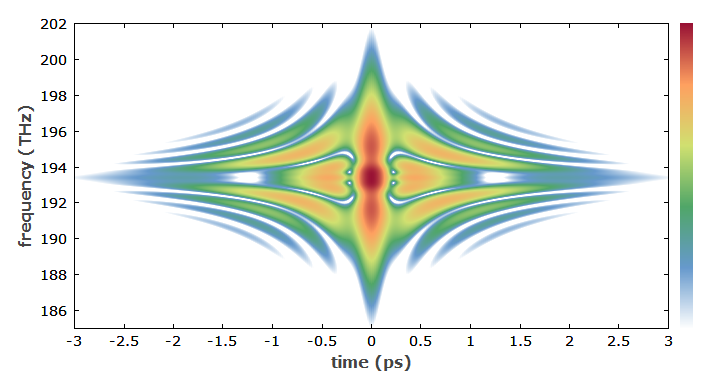
图2:SHG FROG 在光纤中传播一定长度后,对高阶孤子脉冲进行跟踪。 色标(靠近右轴)应用于青蛙强度的对数。 仿真是用RP ProPulse软件完成的。
然后,利用计算机程序实现了一种复杂的迭代相位检索算法,利用FROG轨迹重建脉冲形状。由于记录的数据有很大的冗余性,FROG检索算法不仅可以传递脉冲形状,还可以进行一致性检查。因此,当误差发生时,例如由于光谱仪的错误校准,可能会引起注意。在一台典型的PC上,使用非优化算法,这个过程可能需要几分钟,而优化算法已经开发出来,至少对于形状简单的脉冲,可以在不到0.1秒的时间内完成计算。
术语“频域分辨光学开关”起源于这样一种思想,即短栅极脉冲可用于通过在非线性晶体材料中进行非线性混合(选通)从较长的脉冲中获得样品。 由于通常没有比要研究的脉冲短的附加栅极脉冲,因此FROG实际上使用脉冲本身进行门控。 这使得该方法的应用更加简单,但同时在概念和计算上更加复杂。
频率分辨光学门控的变体
FROG有不同的版本,它们依赖于不同的非线性门控机制,生成不同种类的FROG迹线(因此需要不同的相位检索算法),并且具有不同的优缺点:
- 偏振门控FROG (PG FROG)是概念上最简单的FROG变体 。 在这里,相对于探头脉冲偏振在45°以下的栅极脉冲在重叠时旋转后者的极化χ(3)介质(例如熔融石英),从而导致探头通过偏振器传输。 与FROG一样,用光谱仪分析传输的探头信号。 PG FROG的优点是易于对齐,检索中没有歧义,并且可以生成相当直观的FROG轨迹。 一个问题是需要一个具有非常高消光比的偏振片。
- 在自衍射FROG (SD FROG)中,在χ(3)介质中重叠的两束光束产生非线性折射率光栅 ,将两个光束衍射成新的光束,其中一个用于检测。 由于不需要偏光片,SD FROG可以应用于各种光谱区域,例如深紫外区域。 然而,需要相对较高的脉冲能量。
- 瞬态光栅FROG(TG FROG)也使用非线性折射率光栅,但使用具有可变延迟的第三个脉冲作为探头,该探头在其他两个光束产生的光栅上衍射。 由于各种原因,它允许比SD FROG更高的检测灵敏度。
- 二次谐波FROG (SHG FROG)是最流行的FROG变体 ,如图1所示。 它基于χ(2) 非线性晶体,因此可以达到比所有晶体更高的灵敏度χ(3)青蛙的版本。必须仔细处理相位匹配问题,以避免短脉冲失真。 关于时间方向存在模糊性,可以通过例如在光束路径中使用一些玻璃片进行额外测量来消除。
- 干涉式FROG (IFROG)[12]使用共线几何 ,避免在表征少周期脉冲时因几何效应(有限光束角)而损失时间分辨率。
- 交叉相关FROG (XFROG)[7]使用额外的参考脉冲 ,该脉冲不需要与所研究的脉冲进行光谱重叠。 记录的信号是通过产生两个脉冲的和或差频率获得的。 这种方法可以非常灵敏,并且可以应用于不同的光谱区域。
除了这些传统的FROG测量方法之外,已经开发了FROG的改进版本,甚至可以应用于非常短的脉冲(晶体的角度抖动以消除非线性晶体中群速度不匹配的强烈影响)或相当长的脉冲(需要高光谱仪分辨率)。 GRENOUILLE几何形状[9]实现了特别紧凑的设置,它没有移动部件,甚至可以测量空间啁啾等附加特征。 波导作为非线性分量允许在超低功率水平下进行检测,而偏振加扰使与极化无关的测量成为可能,这有助于例如通过光纤传输脉冲[13]。
频率分辨光学门控的可能替代方案是用于直接电场重建(SPIDER)的光谱相位干涉测量,如光谱相位干涉测量一文所述。
参考文献
[1] D. J. Kane and R. Trebino, “Characterization of arbitrary femtosecond pulses using frequency-resolved optical gating”, IEEE J. Quantum Electron. 29 (2), 571 (1993), doi:10.1109/3.199311
[2] D. J. Kane and R. Trebino, “Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse by using frequency-resolved optical gating”, Opt. Lett. 18 (10), 823 (1993), doi:10.1364/OL.18.000823
[3] FROG tutorial of Rick Trebino's group at the Georgia Institute of Technology, http://www.frog.gatech.edu/tutorial.html
[4] K. W. DeLong et al., “Frequency-resolved optical gating using second-harmonic generation”, J. Opt. Soc. Am. B 11 (11), 2206 (1994), doi:10.1364/JOSAB.11.002206
[5] R. Trebino et al., “Measuring ultrashort laser pulses in the time–frequency domain using frequency-resolved optical gating”, Rev. Sci. Instrum. 68, 3277 (1997), doi:10.1063/1.1148286
[6] A. Baltuška et al., “Amplitude and phase characterization of 4.5-fs pulses by frequency-resolved optical gating”, Opt. Lett. 23 (18), 1474 (1998), doi:10.1364/OL.23.001474
[7] S. Linden et al., “Amplitude and phase characterization of weak blue ultrashort pulses by downconversion”, Opt. Lett. 24 (8), 569 (1999), doi:10.1364/OL.24.000569
[8] L. Gallmann et al., “Collinear type II second-harmonic-generation frequency-resolved optical gating for the characterization of sub-10-fs optical pulses”, Opt. Lett. 25 (4), 269 (2000), doi:10.1364/OL.25.000269
[9] P. O'Shea et al., “Highly simplified device for ultrashort-pulse measurement”, Opt. Lett. 26 (12), 932 (2001), doi:10.1364/OL.26.000932
[10] J. Zhang et al., “Measurement of the intensity and phase of attojoule femtosecond light pulses using Optical-Parametric-Amplification Cross-Correlation Frequency-Resolved Optical Gating”, Opt. Express 11 (6), 601 (2003), doi:10.1364/OE.11.000601
[11] S. Akturk et al., “Extremely simple device for measuring 20-fs pulses”, Opt. Lett. 29 (9), 1025 (2004), doi:10.1364/OL.29.001025
[12] G. Stibenz and G. Steinmeyer, “Interferometric frequency-resolved optical gating”, Opt. Express 13 (7), 2617 (2005), doi:10.1364/OPEX.13.002617
[13] H. Miao et al., “Polarization-insensitive ultralow-power second-harmonic generation frequency-resolved optical gating”, Opt. Lett. 32 (7), 874 (2007), doi:10.1364/OL.32.000874
[14] X. Liu et al., “Numerical simulations of ultrasimple ultrashort laser-pulse measurement”, Opt. Express 15 (8), 4585 (2007), doi:10.1364/OE.15.004585
[15] D. Lee et al., “Experimentally simple, extremely broadband transient-grating frequency-resolved-optical gating arrangement”, Opt. Express 15 (2), 760 (2007), doi:10.1364/OE.15.000760
[16] J. Gagnon et al., “The accurate FROG characterization of attosecond pulses from streaking measurements”, Appl. Phys. B 92, 25 (2008), doi:10.1007/s00340-008-3063-x
[17] R. Trebino, Frequency-Resolved Optical Gating: the Measurement of Ultrashort Laser Pulses, Kluwer, Boston (2002)



