定义
两种透明均质介质界面处透射和反射振幅系数方程。
菲涅耳方程规定了两种透明均匀介质之间界面处的透射和反射振幅系数 - 对于两个不同的偏振方向:
- s偏振:垂直于入射平面的电场矢量(包含所有三个光束的平面,这是图1的绘图平面)
- p 极化:入射平面内的电场矢量
等式为:
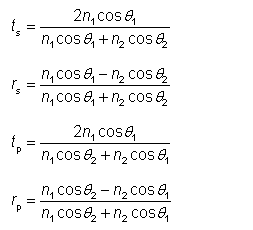
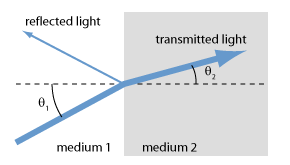
图1:两种介质之间界面处的折射。
例如ts是s极化的振幅传输系数;在这种情况下,传输幅度是入射幅度乘以该因子(不考虑介质中传输的任何相位变化)。n1和n2是两种介质的折射率。 相应的传播角(相对于法线方向测量)为θ1和θ2(见图1)。
例如,幅值传输系数为ts对于S极化,即,如果电场矢量垂直于入射平面。
功率反射系数(反射率或反射率值)只需取相应振幅系数的模平方即可获得。 对于透射率,必须添加一个因子(n2Cosθ2) / (n1Cosθ1)为了考虑到不同的传播角度。
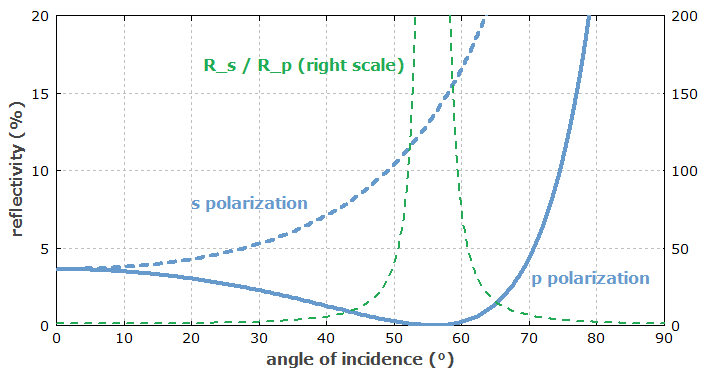
图2:如果光束从空气入射到折射率为 1.47 的介质(例如,1064 nm 处的二氧化硅)上,则 s 和 p 偏振界面的功率反射率。
图2显示了界面的反射率如何取决于入射角和偏振。 如果入射角为布鲁斯特角(此处:≈55.4°),则p偏振的反射系数消失。
对于接口上正常入射的最简单情况,功率反射率(幅度反射率的模数平方)可以用以下公式计算:
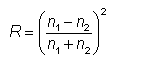
在吸收介质中的应用
菲涅耳方程也可以应用于吸收介质,包括金属。 在这种情况下,需要使用复数折射率;虚部与吸光度有关。 反射系数和透射系数通常不再是实数。
在非正常入射的情况下,计算吸收介质的功率传输会出现困难。 考虑到不同的传播角度,上述校正系数将很复杂,但动力传输系数当然必须是实数。 该问题与光强度不再沿波前恒定的事实有关。



