定义
确定衍射效应机制的参数。
最初,菲涅耳数是在光束传播的衍射理论背景下引入的。 如果光波首先穿过大小(例如半径)a的孔径,然后传播到屏幕的距离L,则情况以菲涅耳数表征。
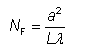
其中λ是波长。
对于远低于1的菲涅耳数值,弗劳恩霍夫衍射发生在屏幕基本上显示孔径的远场衍射图案的地方,这与孔径后光场的复振幅分布的空间傅里叶变换密切相关。
1或更大的菲涅耳数表征了菲涅耳衍射(或近场衍射)的情况,其中数学描述更为复杂。 对于不太大的菲涅耳数和衍射角,可以使用菲涅耳近似。
谐振器的菲涅耳数
菲涅耳数的概念也已应用于光学谐振器(腔),特别是激光谐振器[1]。 再次使用等式
其中a现在是端镜的半径,L是谐振器长度。
谐振器(腔体)的菲涅耳数较大(远高于1)意味着端镜处的衍射损耗对于典型模型尺寸很小(即不接近谐振器的稳定性极限,其中模型尺寸可能会发散)。 这是稳定的激光谐振器的常见情况。 相反,较小的菲涅耳数意味着衍射损耗可能很大 - 特别是对于高阶模式,因此衍射限制操作可能更受青睐。
大多数稳定的激光谐振器具有相当大的菲涅耳数,而较小的菲涅耳数出现在不稳定的谐振器中,有时应用于高功率激光器。
菲涅耳数对于分析延伸到反射镜边缘的(平面)法布里-佩罗干涉仪的模态也很重要。



