定义
用于计算激光增益介质发射截面的方程。
富希特鲍尔-拉登堡方程(通常称为富希特鲍尔-拉登堡方程)是确定激光增益介质发射截面的程序的一部分。 该程序基于与培养基的电子跃迁相关的荧光分析。 波长依赖性荧光强度基本上与发射截面乘以光学频率的三次方成正比。 在发射带宽较小的情况下,后一个因子可以被视为恒定的,因此荧光强度被视为与发射横截面成简单比例。 进一步假设记录的荧光的光谱形状不会通过介质中的波长选择性吸收和放大过程等方式改变。
虽然荧光的光谱形状相对容易测量,但测量绝对值更具挑战性,因为必须知道各种因素,例如掺杂浓度,电子激发程度,收集效率和所用光电探测器的反应。 因此,所获得的横截面光谱的绝对比例通常以某种其他方式获得。 根据Füchtbauer-Ladenburg方法,人们利用了激光跃迁的量子效率通常接近于统一的事实。 这意味着上层状态寿命接近辐射寿命,辐射寿命本身由跃迁到任何低洼能级的发射截面决定。 这由等式定量描述
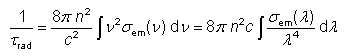
对于逆辐射寿命,其中ν是光学频率,n是折射率,c是光的真空速度,以及σem(ν)表示频率相关的发射截面。 该方程可以被认为是爱因斯坦A和B系数之间关系的扩展。 通过上述窄发射带宽的近似值,这导致
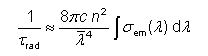
其中支配者包含所考虑跃迁的平均波长。 利用荧光强度I(λ)(例如以W/nm为单位)与发射截面成正比(在狭窄的频率区间内)这一事实,这导致了Füchtbauer-Ladenburg方程
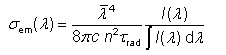
对于带宽较宽的情况,可以通过包含一个因子来使此等式更加准确(λ/λ意味 着)5,考虑到上面已经提到的波长依赖性因素。 如果将强度理解为光子通量,则该校正因子的功率必须降低到4。
请注意,当仅分析光纤中的引导光时,荧光强度函数I(λ)可能会被大幅修改;最好测量侧光中的光谱,以避免吸收、放大和波导效应的任何可能的失真影响。
如果在光谱峰值处将强度归一化为1,则分母中的积分可以解释为有效发射带宽(对于矩形光谱,可以很容易地验证)。
人们应该记住用于富希特鲍尔-拉登堡方程的近似值。 例如,该公式仅适用于相对狭窄的光谱。 此外,重要的是要考虑荧光光谱的所有线。 如果它们分布在相当大的光谱范围内,则无法满足窄带宽的近似值(即使单条线很窄)。 不过,对这种情况进行概括并不困难。
参考文献
[1] W. B. Fowler and D. L. Dexter, “Relation between absorption and emission probabilities in luminescent centers in ionic solids”, Phys. Rev. 128 (5), 2154 (1962), doi:10.1103/PhysRev.128.2154
[2] W. F. Krupke, “Induced-emission cross-sections in neodymium laser glasses”, IEEE J. Quantum Electron. 10, 450 (1974), doi:10.1109/JQE.1974.1068162
[3] B. F. Aull, and H. P. Jenssen, “Vibronic interactions in Nd:YAG resulting in nonreciprocity of absorption and stimulated emission cross sections”, IEEE J. Quantum Electron. 18 (5), 925 (1982), doi:10.1109/JQE.1982.1071611



