定义
激光器的模式锁定,其中多个脉冲在激光谐振器中以相等的时间间隔循环。
有时使用谐波模式锁定技术获得具有高脉冲重复率的脉冲序列,其中多个超短脉冲以恒定的时间间隔在激光谐振器中循环(见图1)。 这种技术通常应用于高(千兆赫兹)脉冲重复率光纤激光器,因为它们的谐振器不能做得足够短,无法通过单个脉冲(→基本模式锁定)实现高重复率。
谐波模式锁定与一些技术挑战有关:
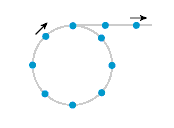
图1:谐波锁模光纤环形激光器示意图。
- 可能需要额外的手段来实现恒定的脉冲能量。 如果没有特殊措施,可能会出现脉冲能量波动,甚至脉冲掉落(脉冲缺失)。
- 循环脉冲并不总是相互相干的,这在某些情况下可能很重要。
- 在被动锁模激光器的情况下,也很难获得稳定的脉冲间隔,即低时序抖动。
各种不稳定性都与所谓的超模噪声有关。 如果谐振器中以相等的相位循环N个相同的脉冲,则只有每N千谐振器模式被激励。 超模噪声意味着无法在这种谐振器模式子集上实现稳定振荡;激光可以跳到不同的模式集,或者在更长的时间内在不同的模式集上表现出同时振荡。 所涉及的节拍音符与高频激光噪声增加有关,例如以时序抖动增加的形式。
有多种方法可以抑制超模噪声。 这些措施包括插入各种类型的腔内光谱滤光片和/或使用电子反馈系统,或利用非线性和色散效应。 在许多情况下,由于这些要求,谐波锁模激光器的设置变得更加复杂。 另一方面,一旦超模噪声得到有效抑制,与基本锁模激光器相比,谐波锁模激光器有可能大幅降低激光噪声(例如定时抖动和相位噪声)。 这主要是因为它们暂时要求单位时间内的激光增益较少,而增益是主要引入时序抖动的原因。
谐波模式锁定的一种变体称为合理谐波模式锁定。 这里,调制频率是往返频率乘以两个整数之比。 这也强制提高了脉冲重复率。 在某些情况下,已经实现了非常高的重复率,但通常具有不恒定的脉冲能量。
参考文献
[1] M. Becker and D. J. Kuizenga, “Harmonic mode locking of the Nd:YAG laser”, IEEE J. Quantum Electron. 8 (8), 687 (1972), doi:10.1109/JQE.1972.1077271
[2] S. Longhi et al., “Third-order-harmonic mode locking of a bulk erbium:ytterbium:glass laser at a 2.5-GHz repetition rate”, Opt. Lett. 19 (23), 1985 (1994), doi:10.1364/OL.19.001985
[3] K. Tamura and M. Nakazawa, “Pulse energy equalization in harmonically FM mode-locked lasers with slow gain”, Opt. Lett. 21 (23), 1930 (1996), doi:10.1364/OL.21.001930
[4] S. Arahira et al., “Mode-locking at very high repetition rates more than terahertz in passively mode-locked distributed-Bragg-reflector laser diodes”, IEEE J. Quantum Electron. 32 (7), 1211 (1996), doi:10.1109/3.517021
[5] A. B. Grudinin and S. Gray, “Passive harmonic mode locking in soliton fiber lasers”, J. Opt. Soc. Am. B 14 (1), 144 (1997), doi:10.1364/JOSAB.14.000144
[6] B. C. Collings et al., “Stable multigigahertz pulse-train formation in a short-cavity passively harmonic mode-locked erbium/ytterbium fiber laser”, Opt. Lett. 23 (2), 123 (1998), doi:10.1364/OL.23.000123
[7] O. G. Okhotnikov and M. Guina, “Colliding-pulse harmonically mode-locked fiber laser”, Appl. Phys. B 72, 381 (2001), doi:10.1007/s003400100529
[8] O. Pottiez et al., “Supermode noise of harmonically mode-locked erbium fiber lasers with composite cavity”, IEEE J. Quantum Electron. 38 (3), 252 (2002), doi:10.1109/3.985565
[9] T. Yilmaz et al., “Supermode suppression to below −130 dBc/Hz in a 10 GHz harmonically mode-locked external sigma cavity semiconductor laser”, Opt. Express 11 (9), 1090 (2003), doi:10.1364/OE.11.001090
[10] Y. Deng and W. H. Knox, “Self-starting passive harmonic mode-locked femtosecond Yb3+-doped fiber laser at 1030 nm”, Opt. Lett. 29 (18), 2121 (2004), doi:10.1364/OL.29.002121
[11] Y. Deng et al., “Colliding-pulse passive harmonic mode-locking in a femtosecond Yb-doped fiber laser with a semiconductor saturable absorber”, Opt. Express 12 (16), 3872 (2004), doi:10.1364/OPEX.12.003872
[12] G. Zhu and N. K. Dutta, “Eighth-order rational harmonic mode-locked fiber laser with amplitude-equalized output operating at 80 Gbits/s”, Opt. Lett. 30 (17), 2212 (2005), doi:10.1364/OL.30.002212
[13] D. Panasenko et al., “Er-Yb femtosecond ring fiber oscillator with 1.1-W average power and GHz repetition rates”, IEEE Photon. Technol. Lett. 18 (7), 853 (2006), doi:10.1109/LPT.2006.871821
[14] S. Zhou et al., “Passive harmonic mode-locking of a soliton Yb fiber laser at repetition rates to 1.5 GHz”, Opt. Lett. 31 (8), 1041 (2006), doi:10.1364/OL.31.001041
[15] S. Gee et al., “Correlation of supermode noise of harmonically mode-locked lasers”, J. Opt. Soc. Am. B 24 (7), 1490 (2007), doi:10.1364/JOSAB.24.001490
[16] Li Zhan et al., “Critical behavior of a passively mode-locked laser: rational harmonic mode locking”, Opt. Lett. 32 (16), 2276 (2007), doi:10.1364/OL.32.002276
[17] G. Sobon et al., “10 GHz passive harmonic mode-locking in Er-Yb double-clad fiber laser”, Opt. Commun. 284 (18), 4203 (2011), doi:10.1016/j.optcom.2011.04.050
[18] V. A. Ribenek et al., “Supermode noise mitigation and repetition rate control in harmonic mode-locked fiber laser implemented through the pulse train interaction with co-lased CW radiation”, Opt. Lett. 47 (19), 5236 (2022), doi:10.1364/OL.472780



