定义
描述激光谐振器中超短脉冲演变的解析方程。
Hermann A. Haus [1] 引入的主方程是物理模型的核心部分,可用于描述锁模激光器谐振器中光脉冲的演变。 该模型的基本思想如下:
- 激光谐振器中循环的光脉冲在时域中以复振幅A(t)描述。 请注意,此功能描述的是单个脉冲,而不是脉冲序列,并且适用于谐振器内的某个位置(例如,就在输出耦合器之前)。 振幅通常归一化,使得A(t)的平方模量是增益介质中的光功率或光强度。
- 然后计算该函数在单个谐振器往返行程内的变化ΔA(t)。 这种变化可能是由激光增益(具有有限增益带宽)、光损耗(由用于主动模式锁定的光调制器或用于被动模式锁定的可饱和吸收器引入的时间依赖性)、色散和光学非线性(例如克尔效应)引起的). 当然,这取决于所考虑的情况,这些影响中哪一个是相关的。 请注意,不考虑与谐振器往返时间相对应的总时间延迟,因此脉冲通常保持在t= 0附近的中心。
- 第一步,振幅一个j(t)可以考虑,其中J表示谐振器往返的次数。 然后将索引j替换为第二个时间变量T = j Trt, 这里T室温是谐振器往返时间。 这导致函数A(T,t)。
- 最后,将T视为一个连续变量,其演化用微分方程描述。 如果每次往返振幅的组合变化为ΔA,则得到的主方程的形式为:
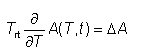
例如,考虑具有腔内色散和Kerr非线性的主动锁模激光器的情况。 在这种情况下,豪斯主方程为:
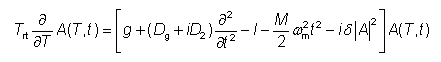
其中,右侧的项(按该顺序)描述了激光增益的恒定部分、增益的频率依赖性和二阶色散、谐振器损耗、时间相关调制器损耗(小时间参数的近似值)和 Kerr 非线性。 这是一个广义的朗道-金茨伯格方程。 主方程可以看作是非线性薛定谔方程的推广,通常用于研究孤子脉冲现象。
近似
重要的是要认识到通常需要哪种近似值:
- 每个谐振器往返的脉冲曲线变化必须很小。 对于许多但不是全部锁模激光器来说,这一条件都得到了很好的满足。 特别是,对于产生低周期脉冲的激光器(例如钛蓝宝石激光器)来说,这是有问题的,其中脉冲参数通常在单个谐振器往返行程内发生较大变化,并且光学元件的顺序很重要。 同样的问题也出现在许多锁模光纤激光器中。
- 所考虑的术语通常不应太复杂,否则可能无法找到分析解决方案(见下文)。 例如,通常省略高阶色散(这将引入三阶或更高阶时间导数)的项,忽略拉曼散射,假设吸收体的饱和度较弱等。
应用
在不太复杂的情况下,豪斯主方程的解析解以稳态(经过多次谐振器往返后得出)而闻名。 例如,没有色散和非线性的主动锁模激光器就是这种情况。 结果是脉冲形状是高斯的,计算出的脉冲持续时间与早期的Kuizenga-Siegman理论完全一致。 也有用Hermite-Gaussian函数描述的高阶解,但这些解每次谐振器往返的净增益较低,因此没有观察到。
在更困难的情况下,可以通过对函数A(t) 使用简单的 ansatz 来获得近似结果,例如对应于塞赫2-形脉冲(可能带有啁啾声)。 这导致了一些方程,例如,人们可以计算脉冲持续时间、线性调频和频谱带宽作为激光参数的函数。
在更复杂的情况下,解析解通常需要近似,其有效性条件在现实情况下通常不能很好地满足。 特别是,由缓慢饱和吸收体引起的时间依赖性损耗很难处理,因为它取决于早期的光强度,因此在Haus Master方程的右侧引入了积分。 另一个问题是解决方案的稳定性;在某些情况下,理论解是动态不稳定的,因此在实践中永远无法观察到。 由于这些原因,数值算法通常用于计算稳态脉冲曲线。 但是,这种方法消除了获取解析方程作为结果的能力,而分析方程在识别参数之间的关系时可能更有帮助。 与使用简单的脉冲传播模型相比,通常没有更多的优势,后者对各种近似值的依赖性较小(见上文),因此能够可靠地描述更广泛的现象。 此外,此类模型的实现和验证并不复杂。
主方程的另一个用途是使用矩法[4]推导有限数量的脉冲参数的动态方程(耦合微分方程),例如脉冲能量,持续时间,线性调频和时间位置。 重点不一定是稳态,而是脉冲参数的演变,例如,可用于研究噪声特性。
总之,Haus Master方程可以被认为是一种有用的工具,主要用于研究可以获得解析解的简单情况,并作为一些动态模型的基础,而简单的脉冲传播模型(依次处理对脉冲的不同影响)通常更适合更复杂的情况,特别是对于被动锁模激光器。
参考文献
[1] H. A. Haus et al., “Structures for additive pulse mode locking”, J. Opt. Soc. Am. B 8 (10), 2068 (1991), doi:10.1364/JOSAB.8.002068
[2] A. M. Dunlop et al., “Pulse shapes and stability in Kerr and active mode-Locking (KAML)”, Opt. Express 2 (5), 204 (1998), doi:10.1364/OE.2.000204 (extended equations, including the transverse spatial dimensions)
[3] H. A. Haus, “Mode-locking of lasers”, J. Sel. Top. Quantum Electron. 6 (6), 1173 (2000), doi:10.1109/2944.902165
[4] N. G. Usechak and G. P. Agrawal, “Rate-equation approach for frequency-modulation mode locking using the moment method”, J. Opt. Soc. Am. B 22 (12), 2570 (2005), doi:10.1364/JOSAB.22.002570
[5] J. Hausen et al., “How carrier memory enters the Haus master equation of mode-locking”, Opt. Lett. 45 (22), 6210 (2020), doi:10.1364/OL.406136
[6] A. M. Perego et al., “Coherent master equation for laser modelocking”, Nature Communications 11, 311 (2020), doi:10.1038/s41467-019-14013-4



