定义
基于参数非线性的光放大过程。
参数放大是一种可以使用参数非线性和泵浦波放大信号的现象。 本文重点介绍光放大,尽管也有电子参数放大器,例如用于微波。 对于光参量放大器,要么χ(2) 某些非线性晶体材料的非线性或χ(3)可以利用非线性,例如光纤[7]。
本文讨论了基于一些光学非线性的参数放大的物理机制。 它不同于通过激发原子、离子或分子的受激发射或半导体激光器中的激发载流子进行激光放大;参数放大不涉及将介质激发到更高的能级(即使一些常用的解释涉及一些虚拟激发态)。 区分简并和非简并参数扩增也很重要,因为它们会导致非常不同的特征。
非简并参数扩增
在这里,我们考虑参数放大基于χ(2)非线性晶体材料,如LiNbO3或三硼酸锂(LBO)。
在非简并情况下,三个不同的光波之间存在相互作用,其角频率为ω1, ω2和ω3(指数按频率值的顺序排列):
- 泵浦波有频率ω3
- 信号波有频率ω2
- 具有频率的所谓空闲波ω1在交互中生成。
出于节能的原因,关系ω3 = ω1 + ω2必须持有。 惰轮频率ω1通常低于信号频率ω2,但它也可以高于此;在任何情况下,信号和惰轮频率都低于泵频率。
信号和惰轮通常具有不同的光学频率,但如果两个波仍然可以通过不同的偏振方向区分,则即使是相同频率的情况也可能被认为是退化的。
从本质上讲,放大过程意味着一些泵浦光子被转换为信号光子和空闲光子。 更准确地说,对于每个消失的泵浦光子,产生一个信号光子和一个空闲光子。 虽然离开非线性晶体的空闲光子通常不使用,但在放大过程中是必不可少的:对于惰波吸收较强的材料,放大器性能会严重下降。
信号幅度的局部增长率不仅与泵浦幅度成正比,而且与已经存在的信号幅度成正比。 因此,该过程可以解释为放大过程 - 例如,与倍频过程不同。
对于平面波或弱聚焦共线高斯光束的简单情况,波与复振幅A1 ~ A3波的非线性相互作用可以用该方程来描述 :
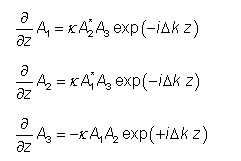
这里
是相位失配(根据波数计算),z是传播方向的坐标,κ是与材料的有效非线性系数成正比的耦合常数。 有时会使用一组更对称的方程,通过将振幅A3替换为iA3可以从上面的方程得到。
最简单的情况是零相位失配(Δk= 0)。 当没有空闲器输入 (A1 = 0 在晶体的开头),在一阶中没有信号放大,也没有任何泵耗尽,而是空闲波的积聚。 如果初始的A3和A2是实数,那么惰轮的实数振幅就会建立起来。(此过程可被视为差频生成。 在下文中,这导致A2 ,即信号放大,然后耗尽泵浦波。
发人深思的东西
非简并参数放大有一个泵浦阈值,而总和频率生成却没有,这难道不奇怪吗? 毕竟,后一个过程不就是另一个过程的时间保留版本吗?
考虑到初始信号的光学相位现在旋转了例如 30°,这是有益的。 这将导致惰轮相位旋转-30°。 因此,添加到信号中的场贡献也会旋转+30°,因此信号像以前一样被放大。 这表明在这种非简并情况下(具有单独的信号和惰轮),放大是相位不敏感的(即与信号相位无关)。
在另一种情况下,泵相旋转30°。 这也会使惰轮旋转 30°。 两个相位变化都抵消了添加到信号中的贡献,因此信号再次被放大,只有空闲相位被改变。
当存在相位不匹配(即非零Δk)时,波的相对相位将在传播过程中发生变化,因此在一定距离后,信号和惰轮的功率可以转换回泵。 因此,只能在有限频率范围内实现的相位匹配对于高效放大非常重要。 在某些特殊条件下,可以实现非常大的相位匹配带宽。
方程还表明,在对惰轮波有强吸收的介质中,信号放大减小,从而使惰轮幅度保持较小。 因此,非线性晶体的透明度范围必须足够大,以使惰波保持在低损耗窗口内,即使对惰波本身不感兴趣。 然而,在某些情况下,一定程度的惰轮吸收甚至可能是有益的[9]。
使用的方程基于经典物理学。 在量子力学图片中,存在泵浦光子转换为信号空闲光子对的过程。 这些是强相关的,导致非经典统计。
简并参数放大
在很少使用的简并情况下,信号波和空闲波不仅在频率上而且在极化上都是相同的,即它们无法区分。 因此只有信号幅值A1和泵浦幅值A2,并且没有惰轮 。 然后,信号波长正好是泵浦波长的两倍。 相互作用用方程描述
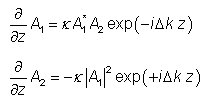
和
在这里,放大是相位敏感的。 例如,如果信号和泵浦幅度为实且为正,则会发生信号放大(对于零相位不匹配),或者当泵浦幅度的符号发生变化时,会发生信号去放大。 能量转移的方向由该项的复相决定 A12 A2* 。
相敏放大提供了一种产生所谓的光挤压状态(例如挤压真空)的机制,并且原则上它允许人们避免过多的放大器噪声,即将噪声系数保持在1附近。 然而,由于需要在泵浦和信号之间保持固定的相位关系,使得这种光放大太不方便,例如用于光纤通信。
光纤中的参数放大
由于材料的中心对称性,玻璃纤维不表现出χ(2)非线性(除非在某些情况下,例如当光纤被强电场“极化”时)。 然而,参数放大也可能由于χ(3)非线性。 在这种情况下,可能涉及四种不同的频率:两个泵频率、一个信号频率和一个惰轮频率。 一个常见的情况是部分简并,其中只有一个泵波。
由于信号和惰轮的光相位受到交叉相位调制(XPM)和光纤的色散的影响,因此相互作用有些复杂。 (对于强信号,还会发生自相位调制。 参数放大仅在泵浦波长周围的某个波长范围内获得。 当色散较弱时,该范围可能相当宽,其宽度取决于泵浦功率。

图1:群速度色散为 −2000 fs 的 1 m 光纤的参数增益光谱2/m 表示 1300 nm 处泵浦波的不同功率。
图1显示了一个示例案例的增益频谱。 最高增益发生在信号波长处,其中相位匹配是通过相互消除XPM和色散效应获得的。 这仅适用于异常色散。
通过使用高度非线性的光纤,可以最大限度地减少所需的光纤长度。 这也具有相位匹配更容易实现且对温差等外部影响不太敏感的优点。
参数增益主要与短光脉冲在光纤中传播的情况有关。 数值脉冲传播建模可以模拟各种效应可以发挥作用的情况。 例如,由于群速度失配和孤子效应而导致脉冲的部分时间重叠。 多模光纤中的相互作用特别复杂,因为不同的传播模式组合的相位匹配是不同的。
参考文献
[1] N. M. Kroll, “Parametric amplification in spatially extended media and application to the design of tuneable oscillators at optical frequencies”, Phys. Rev. 127 (4), 1207 (1962), doi:10.1103/PhysRev.127.1207
[2] R. H. Kingston, “Parametric amplification and oscillation at optical frequencies”, Proc. IRE 50, 472 (1962)
[3] S. A. Akhmanov and R. V. Khokhlov, “Concerning one possibility of amplification of light waves”, Sov. Phys. JETP 16, 252 (1963)
[4] S. A. Akhmanov et al., “Observation of parametric amplification in the optical range”, JETP Lett. 2, 191 (1965)
[5] B. R. Mollow and R. J. Glauber, “Quantum theory of parametric amplification. I”, Phys. Rev. 160 (5), 1076 (1967), doi:10.1103/PhysRev.160.1076
[6] R. A. Baumgartner and R. L. Byer, “Optical parametric amplification”, IEEE J. Quantum Electron. 15 (6), 432 (1979), doi:10.1109/JQE.1979.1070043
[7] R. H. Stolen and J. E. Bjorkholm, “Parametric amplification and frequency conversion in optical fibers”, IEEE J. Quantum Electron. 18 (7), 1062 (1982), doi:10.1109/JQE.1982.1071660
[8] G. Arisholm, T. Südmeyer, and R. Paschotta, “Limits to the power scalability of high-gain optical parametric oscillators and amplifiers”, J. Opt. Soc. Am. B 21 (3), 578 (2004), doi:10.1364/JOSAB.21.000578
[9] G. Rustad et al., “Effect of idler absorption in pulsed optical parametric oscillators”, Opt. Express 19 (3), 2815 (2011), doi:10.1364/OE.19.002815
[10] R. L. Sutherland, Handbook of Nonlinear Optics, 2nd edn., Marcel Dekker, New York (2003)
[11] R. W. Boyd, Nonlinear Optics, Academic Press, 2nd edn., CRC Press, Boca Raton, FL (2003)
[12] G. P. Agrawal, Nonlinear Fiber Optics, 4th edn., Academic Press, New York (2007)



