定义
温度梯度引起的透镜效应。
特别是在高功率激光器中,增益介质(例如激光晶体)的不均匀加热通常通过以下机制导致显着的热透镜(即聚焦作用):
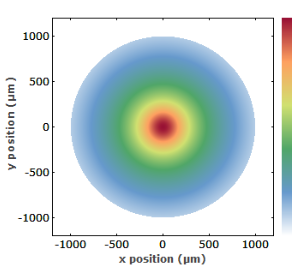
图1:从泵浦端看到的端部泵浦激光圆柱形晶体中的温度曲线。最高温度发生在光束轴周围。由于外表面的冷却,存在热流,因此不可避免地在径向方向上出现温度梯度。
- 与外部区域相比,增益介质在光束轴上更热,通常会导致折射率的一些横向梯度(热光学效应,用系数dn / dT量化)。
- 热引起的机械应力可能导致进一步的折射率变化(光弹性效应,用光弹性系数量化ρij和热膨胀系数α)。
- 机械应力也会导致增益介质的端面凸出,因此也会导致透镜。 这种效应对于短激光晶体可能很重要。
根据情况,这些影响可能具有不同的相对强度甚至迹象。 在许多激光晶体中,首先提到的效应(折射率的温度依赖性)是最重要的。
请注意,热透镜不仅可能发生在激光增益介质中,还可能发生在其他光学元件中,例如Q开关和其他光调制器,拉曼活性晶体,法拉第隔离器,甚至通过基板凸出的介电镜。
热透镜带来的挑战
原则上,即使是强热透镜也可以通过调整所用激光谐振器的设计来补偿 - 例如,在激光晶体旁边使用凸(散焦)激光镜。 然而,热透镜会给激光设计带来各种挑战:
- 热透镜的屈光度取决于泵浦功率,在某种程度上还取决于腔内激光功率。 (后一种依赖性可以有任一符号,具体取决于激光增益介质和工作波长的细节。 对于具有非常高输出功率的激光器,即使功率水平的微小变化也可能使热透镜的屈光度功率发生很大变化,以至于激光谐振器的模式特性会大幅改变。 谐振器甚至可能变得不稳定,因此激光器甚至可能停止运行。
- 虽然原则上可以计算热透镜的屈光度,但在实践中通常存在很大的不确定性,例如由于未知的材料细节、复杂的几何形状或不完美(可能可变)的热接触。 热透镜还取决于激光晶体的质量,而激光晶体的质量可能是可变的。
- 通常,热透镜会产生大量的光学像差。 对于端泵浦激光器尤其如此,对于侧泵浦激光器来说,情况暂时较小。 这一方面会使实现高光束质量变得更加困难,并且功率转换效率也会受到影响。
- 在具有强热透镜的情况下,激光的对准可能会变得更加困难。 在极端情况下,对齐的微小变化会改变热透镜的特性,甚至可能出现多稳态行为。
屈光度功率的计算
为了计算热透镜的屈光度功率,首先需要计算耗散功率。 这是吸收的泵功率的一定百分比。 这个百分比有多大,取决于具体情况。 在像Yb掺杂光纤激光器这样的简单情况下,激光活性离子除了对泵浦和激光跃迁的吸收和发射外几乎不能做任何其他事情,并且自发发射通常对加热的影响很小,人们可以相对容易地计算基于量子缺陷的加热。 例如,在其他情况下,可能发生额外的淬火和上转换过程,计算更加困难,并且可能存在很大的不确定性。
此外,热透镜效应在很大程度上取决于泵送和冷却几何形状。 举一个简单的例子,考虑一种各向同性的激光增益介质,其中具有均匀的泵浦强度和纯径向热流。 (这种情况可能发生,例如在侧面泵浦激光棒中。 然后,我们有一个具有屈光度(反焦距)的热透镜)
这里P热是耗散功率,A是泵浦面积,κ是导热系数。 增益介质的长度无关紧要,在这种情况下,热透镜没有像差。
该方程似乎表明,使用较大的泵浦面积和相应的更大谐振器模式工作会降低透镜效应,但大模式对热透镜更敏感,这恰好补偿了明显的优势。 该方程还表明,对于高功率增益介质,有用的品质因数是(dn / dT)/κ的比值,该比率应尽可能小。 当然,泵功率转换为热量的比例也应尽可能小。
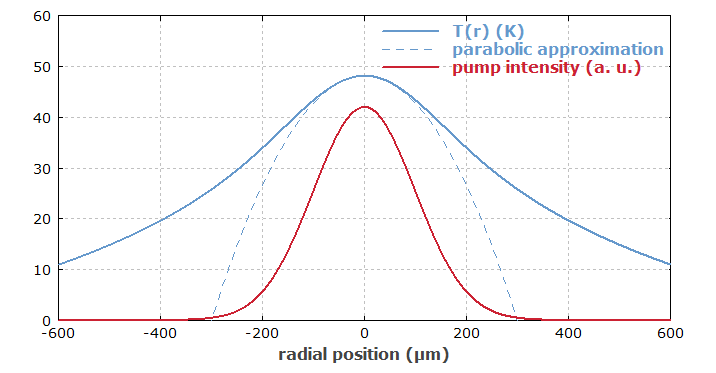
图2:横向泵强度分布(红色)和热曲线(蓝色),模拟了 8 mm 长的端泵Nd:YAG棒,耗散功率为 14 W。 假设光束方向的分布是均匀的,这对于双向泵浦和不太强的泵浦吸收大致正确。 温度曲线仅在晶体中心附近近似抛物线,因此光束半径等于泵浦光束半径的激光模式将经历一些像差。
对于耗散功率的非均匀分布,热透镜通常会出现光学像差(见图1)。 这在端面泵浦激光器中经常是一个问题。 例如,当使用高斯强度分布泵浦时,光束轴上的热透镜比根据有效模面积的上述公式计算的热透镜强两倍,但在较大的半径下会下降。
许多激光晶体表现出dn / dT的正值,数量级为10−6 K−1,但有些(例如Nd:YLF)具有负温度系数,如果该效应没有被应力效应过度补偿,则会导致散焦透镜。 另外,拉曼晶体材料Ba(NO3)2(氮化钡)具有强负dn / dT和低导热性,导致强烈的散焦,例如在腔内拉曼位移激光器中。
计算热透镜强度的可靠数据通常很难获得,即使对于相对知名的晶体材料也是如此。 主要是由于与测量此类特性相关的各种技术困难,文献中经常出现不准确的数据。 此外,还有一个与数量dn / dT相关的更基本问题:在各种理论计算中,应使用恒定应变条件下折射率的偏导数,而测量数据通常适用于恒定应力[20]。 这些值之间的差异可能很大,源于还存在热膨胀的事实。 因此,使用从热透镜测量得出的有效热光学系数可能更明智。 即便如此,也不容易区分端面凸起的影响,其重要性取决于晶体几何形状。
对热透镜的深入分析通常需要先进的方法,例如有限元分析(FEA)来计算激光晶体中的温度和应力场。 例如,在设计复合激光晶体(见下文)时,了解其他未掺杂部件的效果如何取决于其尺寸非常重要。 然而,在许多情况下,此类计算受到缺乏数据的困扰,例如关于精确的泵强度分布、介质和机械接触的热特性、增益介质中的淬火效应等,因此通常难以实现高精度的结果。 因此,使用基于各种简化假设的更务实的方法处理估计通常是有利的,这大大减少了所需的工作量,并且仍然为实验提供了有用的指导。 理论结果可以补充实验数据,以校准某些参数。
几何的影响
对于其他几何形状的激光,热透镜的屈光度功率对光束区域的依赖性可能不同,例如在薄盘激光器中。 至少部分纵向的热流,从而减少热透镜也可以通过透明散热器来实现,例如由金刚石制成的。
几何形状的这种影响在激光器功率缩放的背景下非常重要,并且它们的理解可能比例如对任何特定配置的温度曲线进行复杂计算更有帮助。
应对激光器中的热透镜
原则上,在激光谐振器的设计中可以考虑热透镜。 困难在于热透镜的屈光度取决于泵浦功率,并且热透镜通常具有明显的像差。 这会使获得良好的光束质量变得困难。 然而,良好的谐振器设计可以极大地帮助减少热透镜的影响。 谐振器设计应使热透镜的变化不会对激光谐振腔中的振型尺寸产生太大影响,并且热透镜的像差仅产生很小的影响。 也可以用激光谐振器中的其他光学元件补偿像差。
热透镜的强度可以通过多种方式降低:
- 通过使用具有低功率损耗、高导热性和小热光学系数的增益介质
- 通过选择泵浦和激光波长以获得小的量子缺陷
- 通过增益介质(→低温激光器)的低温冷却,显著改善了几个参数,对热透镜有影响
- 通过优化泵浦梁的形状
- 通过优化激光头的几何形状,例如通过薄盘激光器中的纵向散热,或使用复合激光晶体
- 通过采用波导结构作为增益介质;例如,光纤激光器在很大程度上不受热透镜效应的影响,除非在非常高(几千瓦)的输出功率水平下。
如果发生透镜效应并且谐振器中的位置不同,则它们的影响不一定加起来,具体取决于透镜的分布方式;它们甚至可能部分相互抵消。
与热透镜相关的现象是热诱导双折射,这可能导致去极化损耗和偏振依赖性散光。
激光外部的热透镜
当具有高平均功率的激光束通过透明光学设备(如透镜、分束器或保护窗或法拉第隔离器)发送时,热透镜在激光谐振器之外也可能很重要。 因此,焦点在这种元件后面的位置可能取决于光功率水平。 例如,在高功率激光切割头中,可能会发生这种情况。
热透镜的无源补偿
可以构建表现出具有反向符号的热透镜的光学元件,即随光功率增加的散焦作用[16]。 例如,可以通过流体层表现出负值dn / dT来实现。 这些元件可用于补偿聚焦热透镜,例如在激光谐振器或某些高功率聚焦光学器件中。
光纤中的热透镜
光纤在很大程度上不受热透镜的影响。 这是因为热透镜通常太弱,无法实质性地改变光纤模式的特性。 然而,在极端情况下,由于每米光纤的热负荷非常高,并且模式面积也非常大,热透镜可以显着改变有效模式区域,甚至将光纤从单模状态带到多模状态[23]。
参考文献
[1] W. Koechner, “Thermal lensing in a Nd:YAG laser rod”, Appl. Opt. 9 (11), 2548 (1970), doi:10.1364/AO.9.002548
[2] T. Kimura and K. Otsuka, “Thermal effects of a continuously pumped Nd3+:YAG laser”, IEEE J. Quantum Electron. 7 (8), 403 (1971), doi:10.1109/JQE.1971.1076822
[3] J. Steffen et al., “Fundamental mode radiation with solid-state lasers”, IEEE J. Quantum Electron. 8 (2), 239 (1972) , doi:10.1109/JQE.1972.1076948
[4] B. Bendow and P. D. Gianino, “Optics of thermal lensing in solids”, Appl. Opt. 12 (4), 710 (1973), doi:10.1364/AO.12.000710
[5] V. Magni, “Multielement stable resonators containing a variable lens”, J. Opt. Soc. Am. A 4 (10), 1962 (1987), doi:10.1364/JOSAA.4.001962
[6] D. Metcalf et al., “Laser resonators containing self-focusing elements”, Appl. Opt. 26 (21), 4508 (1987), doi:10.1364/AO.26.004508
[7] S. De Silvestri et al., “Rod thermal lensing effects in solid-state laser ring resonators”, Opt. Commun. 65 (5), 373 (1988), doi:10.1016/0030-4018(88)90106-X
[8] M. E. Innocenzi et al., “Thermal modeling of continuous-wave end-pumped solid-state lasers”, Appl. Phys. Lett. 56, 1831 (1990), doi:10.1063/1.103083
[9] W. Winkler et al., “Heating by optical absorption and the performance of interferometric gravitational-wave detectors”, Phys. Rev. A 44 (11), 7022 (1991), doi:10.1103/PhysRevA.44.7022
[10] H. J. Eichler et al., “Thermal lensing and depolarization in a highly pumped Nd:YAG laser amplifier”, J. Phys. D: Appl. Phys. 26, 1884 (1993), doi:10.1088/0022-3727/26/11/008
[11] L. Yan and C. H. Lee, “Thermal effects in end-pumped Nd:phosphate glasses”, J. Appl. Phys. 75 (3), 1286 (1994), doi:10.1063/1.356405
[12] J. L. Blows et al., “Heat generation in Nd:YVO4 with and without laser action”, IEEE Photon. Technol. Lett. 10 (12), 1727 (1998), doi:10.1109/68.730483
[13] N. Hodgson et al., “High power TEM00 mode operation of diode-pumped solid-state lasers”, Proc. SPIE 3611, 119 (1999), doi:10.1117/12.349265
[14] P. J. Hardman et al., “Energy-transfer upconversion and thermal lensing in high-power end-pumped Nd:YLF laser crystals”, IEEE J. Quantum Electron. 35 (4), 647 (1999), doi:10.1109/3.753670
[15] R. Paschotta et al., “Thermal effects in high-power end-pumped lasers with elliptical-mode geometry”, J. Sel. Top. Quantum Electron. 6 (4), 636 (2000), doi:10.1109/2944.883378
[16] E. Wyss et al., “Thermooptical compensation methods for high-power lasers”, IEEE J. Quantum Electron. 38 (12), 1620 (2002), doi:10.1109/JQE.2002.805105
[17] S. Chénais et al., “Thermal lensing in diode-pumped ytterbium lasers – Part I: theoretical analysis and wavefront measurements”, IEEE J. Quantum Electron. 40 (9), 1217 (2004), doi:10.1109/JQE.2004.833198
[18] R. L. Aggarwal et al., “Measurement of thermo-optic properties of Y3Al5O12, Lu3Al5O12, YAlO3, LiYF4, LiLuF4, BaY2F8, KGd(WO4)2, and KY(WO4)2 laser crystals in the 80–300 K temperature range”, J. Appl. Phys. 98 (10), 103514 (2005), doi:10.1063/1.2128696
[19] G. Wagner et al., “Simulations of thermal lensing of a Ti:sapphire crystal end-pumped with high average power”, Opt. Express 13 (20), 8045 (2005), doi:10.1364/OPEX.13.008045
[20] S. Chénais et al., “On thermal effects in solid-state lasers: the case of ytterbium-doped materials”, Prog. Quantum Electron. 30 (12), 89 (2006), doi:10.1016/j.pquantelec.2006.12.001
[21] A. Soloviev et al., “Experimental study of thermal lens features in laser ceramics”, Opt. Express 16 (25), 21012 (2008), doi:10.1364/OE.16.021012
[22] P. A. Loiko et al., “Thermo-optic coefficients and thermal lensing in Nd-doped KGd(WO4)2 laser crystals”, Appl. Opt. 49 (34), 6651 (2010), doi:10.1364/AO.49.006651
[23] K. R. Hansen et al., “Thermo-optical effects in high-power ytterbium-doped fiber amplifiers”, Opt. Express 19 (24), 23965 (2011), doi:10.1364/OE.19.023965
[24] I. I. Kuznetsov et al., “Thermal effects in end-pumped Yb:YAG thin-disk and Yb:YAG/YAG composite active element”, IEEE J. Quantum Electron. 50 (3), 133 (2014), doi:10.1109/JQE.2013.2297743
[25] L. Lang et al., “Silicate bonding of sapphire to SESAMs: adjustable thermal lensing for high-power lasers”, Opt. Express 29 (12), 18059 (2021), doi:10.1364/OE.427192
[26] W. Koechner, Solid-State Laser Engineering, 6th edn., Springer, Berlin (2006)



