定义
弱引导近似中具有径向对称折射率曲线的光纤的线偏振模态。
许多光纤的横向折射率分布是径向对称的,即折射率仅取决于径向坐标r,而不取决于方位坐标φ。 此外,几乎所有光纤(光子晶体光纤除外)的折射率分布仅表现出很小的折射率对比度,因此可以假设光纤仅具有弱导向性。 在这种情况下,光纤模式的计算大大简化。 一种获得线性极化LP模式。
在引导较强的情况下,需要区分TE和TM模式,其中只有电场或磁场正好垂直于光纤轴。 还有HE型和EH型的混合模式,具有非零的电场和磁场的纵向分量。 例如,这种不弱引导光纤的情况适用于纳米纤维,其中玻璃/空气界面提供波导功能。
LP 模式的计算
圆柱坐标中复电场剖面E(r,φ)的波动方程为:
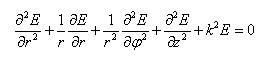
其中k= 2π n/λ 是局部折射率n和真空波长λ 产生的波数。 在纤维中,该量通常在空间上是变化的 - 并且根据我们的特定假设仅取决于径向坐标r。
寻找相位常数β(传播常数的虚部,对于给定的真空波长λ仍有待确定)的模式,我们得到:
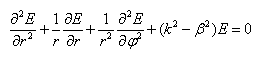
由于径向对称性,我们可以使用 ansatz
其中l需要是一个整数(因为否则φ依赖因子将不是连续的)。 我们可以使用相同的 ansatz 与因子 sin l φ 而不是 cos l φ,或者实际上是它们的某种线性组合,或者使用exp(±i l φ),但得到的径向方程在任何情况下都是
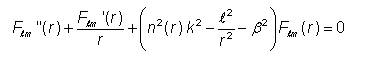
对于给定的波长,仅对于某些离散值β径向方程具有在r → ∞收敛于零的解。 只有这样的解决方案才能代表光纤的引导模式。 这些对应于引导模式的β值称为βlm,其中l 是选定的方位角指数(见上文),索引m从 1(对于可能的最高β值)开始,范围到某个最大值,随着l 的增加,该值趋于减小。 一旦l变得太高,就根本没有解决方案。 然后,可以通过从 l= 0 开始找到所有引导模式,找到所有β值,然后执行此操作以增加l值,直到不再有解决方案。
阶跃折射率光纤
对于更具体的情况,阶梯折射率光纤(其中光纤芯内的折射率恒定),可以找到径向方程的纤芯和包层部分的解析解。 核心部分涉及贝塞尔函数Jℓ(你是/r核心),和包层部分修改贝塞尔函数Kℓ(W r/r核心))哪里
和
必须平衡芯和包层部分的预因,以使功能在核心/包层接口处连续。
人们很容易认识到
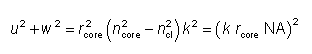
其中 NA 是数值孔径。
LP 模式的属性
阶跃折射率光纤
所有引导模式都有β值,这些值位于核心和包层的平面波数之间。 β值接近下限(包层波数)的模式具有较小的w参数,导致包层中的径向函数缓慢衰减。
可以将光纤的有效折射率计算为β除以真空波数。 对于引导模式,该有效折射率介于芯和包层的折射率之间。
最低阶模式 (LP01)的强度分布类似于高斯光束的强度分布,特别是在V数不太高的情况下。 特别是对于较高的m值,产生的径向函数可以在光纤芯中振荡,而在包层中衰减或多或少。 图 1 显示了一个示例案例的径向函数。 在这里,我们有两种模式,l = 0(LP01, LP02) 和 l = 1 和l =2 各一个模式。 请注意,对于每个非零 l 值,我们有两个线性独立的解,分别具有cosl φ 和sin lφ依赖性,或者依赖于exp(i lφ)。 考虑到这一点,在我们的示例示例中,我们总共有 2 + 2 + 2 = 6 种模式。
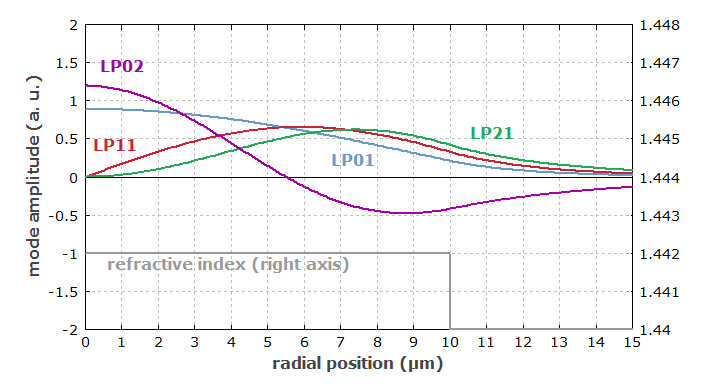
图1:阶跃折射率光纤的光纤模式的径向函数。
光纤的V数越高,存在的引导模式就越多。 对于低于2.405的V,只有一个引导模式(除了不同的偏振方向),所以我们有一个单模光纤。 对于大V,模式数与V2. 图2显示了V数较高(11.4)的阶跃折射率光纤所有模态的复振幅曲线。
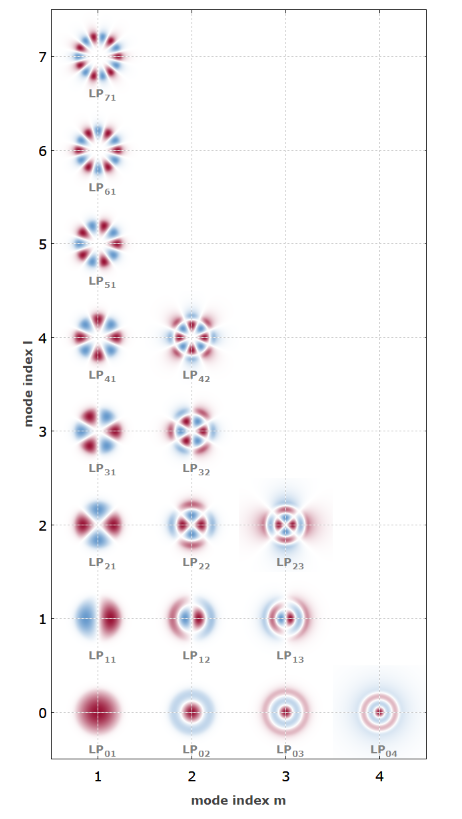
图2:阶跃折射率光纤所有引导模式的电场幅度曲线。 这两种颜色表示电场值的不同符号。 此图(与所有其他图表一样)是使用软件 RP 光纤功率生成的。
在此示例中,LP23和 LP04模式相对接近它们的截止值:它们将不再存在,只有稍长的波长。 在这种情况下,w参数变得非常小,因此磁场更多地渗透到包层中。 例如,这种模式对弯曲损耗可能更敏感。 但是,仅对于l = 0的模式,内核中传播的功率在截止时消失。
具有其他折射率曲线的光纤
对于任意径向折射率曲线,引导模式仍然可以计算为 LP 模式,即使它们的形状可能与步进折射率光纤的形状有很大偏差。 通常需要一种数值方法来查找引导模式的径向解,至少对于核心部分;修改后的贝塞尔函数仍可用于折射率恒定的包层部件。 对于核心部件,可以始终从r= 0开始,将场传播到核心/包层接口(例如,使用Runge-Kutta算法),并将其与包层部件的修改贝塞尔函数连接。 接口处导数的不匹配可以通过数值细化β值来最小化。 需要实施一个数值策略来查找不匹配消失的所有β值。
由于各种技术细节,数值计算并非完全微不足道。 至少如果需要高计算速度,则必须根据每种模式的参数仔细确定所需的数值步长。 这同样适用于数值根查找的参数。
当然,整个方法不能再应用于非径向对称的折射率轮廓;然后必须参考二维数值方法,这些方法处理起来要复杂得多,并且需要更多的计算时间。
图 2 显示了一个示例案例的计算模式函数。
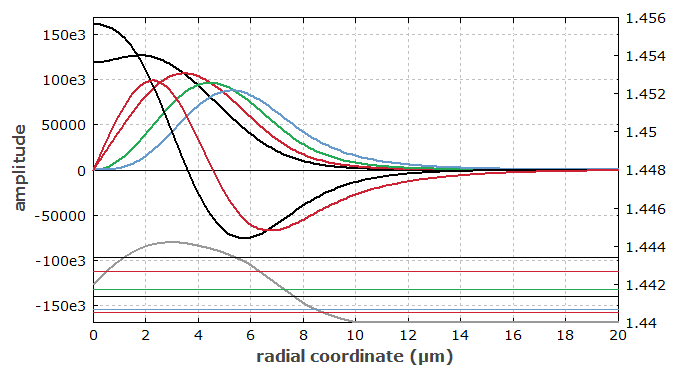
图3:根据GeO浓度确定的具有平滑折射率分布的情况计算的光纤模式的径向函数2在二氧化硅纤维的核心。
传播速度和色散
模态的相速度只是光的真空速度除以有效折射率(见上文)。 群速度是β值相对于角频率的导数的倒数。 因此,对于群速度的数值计算,需要计算至少两个不同(紧密间隔)波长的模态。 为了考虑材料色散,需要使用与波长相关的折射率。
群速度色散是β值相对于角频率的二阶导数。 从数字上讲,至少需要三种不同波长的β值。 请注意,对于小波长间距,计算β值需要非常高的精度。
轨道角动量
基于具有exp(±i lφ)(见上文)的框架函数与每光子±lh/2π的轨道角动量相关。
折射率曲线的优化
通过优化光纤的折射率分布,可以改善LP模式的许多重要参数。 例如,可以实现所需的模态大小和模态数量,但也强烈修改群速度和色散。 为了最小化模态耦合效应,可以注意相关模态的β值不要太接近。用于计算光纤模式的灵活软件可以成为此类优化的重要工具。



