定义
放大光功率调制的非线性光学效应。
调制不稳定性可能由不同类型的非线性引起。 在光学方面,特别是在非线性光纤中,它们通常是由光纤的克尔非线性与异常色散引起的。 从本质上讲,它们意味着光谱中边带的放大,并导致光功率的振荡增加。
数学描述
在最简单的情况下,人们考虑光的一维传播,例如在单模光纤中。 在某个纵向位置z和时间t处的光可以简单地用复振幅A(t,z)来描述,模数平方就是光功率。 如果唯一相关的物理效应是克尔非线性,则用非线性系数γ(以rad/(W m)为单位)和与频率无关的群速度色散量化 β2(即,没有高阶色散,没有传播损失等),传播可以用非线性薛定谔方程描述:

基于该方程,可以相对容易地表明,小的正弦幅度随频率调制ωm添加到恒定振幅(带功率P= |答|2) 可以放大,如果满足以下条件:
这显然是可能的,如果β2 < 0(异常色散)和光功率足够高。 调制的增益系数可以计算为

其中平方根下的第一个项是正数,因为β2 < 0. 请注意,如果不满足上述条件,则增益为零;然后是纯粹的振荡行为。
由此产生的非线性增益可以解释为通过相位匹配的四波混合进行参数放大的结果。
示例案例
例如,我们考虑一种情况,即具有微弱甚高频调制(4 THz)的光信号被注入具有异常色散的无源单模光纤中。 只有在超短脉冲的短时间间隔(例如20 ps)内,我们假设平均功率相当高(3.5 kW)。 通过这种方式避免了受刺激布里渊散射的问题。
原始脉冲的光谱(图1)显示了围绕中心光谱分量的两个弱旁瓣,并且存在量子涨落产生的噪声背景:
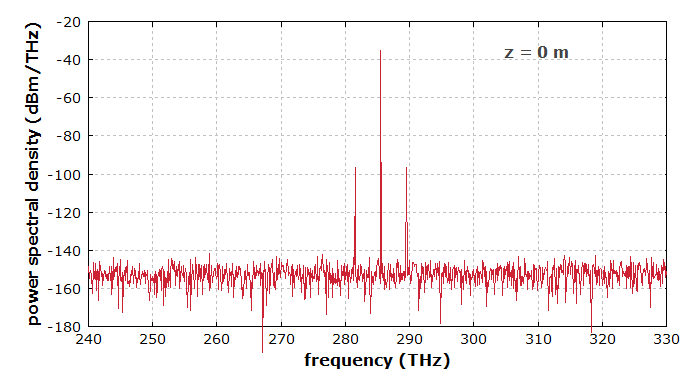
图1:输入光的光谱。
下图显示了0.2 m光纤后的情况,表现出与显着放大的功率振荡相关的旁瓣增加(未显示)。 此外,量子噪声背景在中心波长周围放大了几太赫兹:

图2:0.2 m光纤后的光谱。
在0.4米的光纤之后,旁瓣再次变强,噪声放大也变得更加明显:

图3:0.4 m光纤后的光谱。
0.6 m 光纤后:
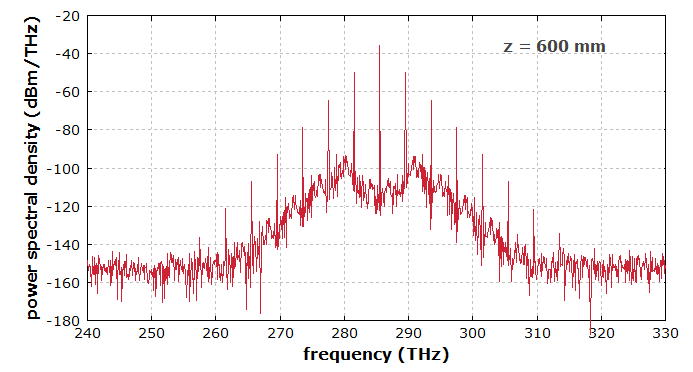
图4:0.6 m光纤后的光谱。
仿真已使用软件RP光纤功率完成。

图5:不同光功率电平的调制不稳定性增益。
图5显示了三种不同光功率水平的调制增益或不稳定性。 人们可以看到,功率的增加不仅扩展了非线性增益的幅度,还扩展了频率范围。
下图显示了在时域中产生的放大调制。 它比输入调制强得多,不再是正弦的,并且表现出随机量子噪声的一些影响:
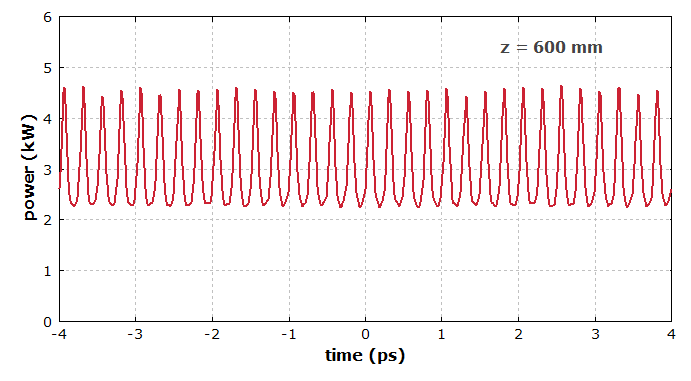
图6:0.6 m光纤后的时域调制,对应于最后显示的频谱。
调制不稳定性的变化
更复杂的调制不稳定性现象可能发生在各种情况下。 例如,即使在色散处于正常色散状态,也可以在双折射光纤中观察到它;这称为矢量调制不稳定性。 此外,如果光纤不具有单模设计,则效应可能涉及额外的光纤模式,并且可能通过交叉相位调制以各种形式发生。
调制不稳定性也经常在超连续体生成的背景下发挥作用,然而相互作用效应的复杂性要大得多。 在这种情况下,调制或不稳定只是众多影响之一。 例如,它可以参与拉曼孤子的形成。
在某些电信系统中观察到与调制或不稳定有关的问题。 即使在正常的色散状态下,在用光纤放大器定期提高信号功率的系统中也会出现此类问题。 这种周期性变化会导致一种准相位匹配。
参考文献
[1] P. K. Shukla and J. Juul Rasmussen, “Modulational instability of short pulses in long optical fibers”, Opt. Lett. 11 (3), 171 (1986), doi:10.1364/OL.11.000171
[2] M. Nakazawa, K. Suzuki and H. A. Haus, “Modulational instability oscillation in nonlinear dispersive ring cavity”, Phys. Rev. A 38, 5193 (1988), doi:10.1103/PhysRevA.38.5193
[3] S. Trillo and S. Wabnitz, “Dynamics of the nonlinear modulational instability in optical fibers”, Opt. Lett. 16 (13), 986 (1991), doi:10.1364/OL.16.000986
[4] G. G. Luther and C. J. McKinstrie, “Transverse modulational instability of counterpropagating light waves”, J. Opt. Soc. Am. B 9 (7), 1047 (1992), doi:10.1364/JOSAB.9.001047
[5] E. A. Golovchenko and A. N. Pilipetskii, “Unified analysis of four-photon mixing, modulational instability, and stimulated Raman scattering under various polarization conditions in fibers”, J. Opt. Soc. Am. B 11 (1), 92 (1994), doi:10.1364/JOSAB.11.000092
[6] C. M. de Sterke, “Theory of modulational instability in fiber Bragg gratings”, J. Opt. Soc. Am. B 15 (11), 2660 (1998), doi:10.1364/JOSAB.15.002660
[7] P. M. Lushnikov, P. Lodahl and M. Saffman, “Transverse modulational instability of counterpropagating quasi-phase-matched beams in a quadratically nonlinear medium”, Opt. Lett. 23 (21), 1650 (1998), doi:10.1364/OL.23.001650
[8] S. Pitois, M. Haelterman and G. Millot, “Bragg modulational instability induced by a dynamic grating in an optical fiber”, Opt. Lett. 26 (11), 780 (2001), doi:10.1364/OL.26.000780
[9] G. Millot, “Multiple four-wave mixing-induced modulational instability in highly birefringent fibers”, Opt. Lett. 26 (18), 1391 (2001), doi:10.1364/OL.26.001391
[10] T. Tanemura and K. Kikuchi, “Unified analysis of modulational instability induced by cross-phase modulation in optical fibers”, J. Opt. Soc. Am. B 20 (12), 2502 (2003), doi:10.1364/JOSAB.20.002502
[11] S. Longhi, “Modulational instability and space-time dynamics in nonlinear parabolic-index optical fibers”, Opt. Lett. 28 (23), 2363 (2003), doi:10.1364/OL.28.002363
[12] A. Armaroli and S. Trillo, “Modulational instability due to cross-phase modulation versus multiple four-wave mixing: the normal dispersion regime”, J. Opt. Soc. Am. B 31 (3), 551 (2014), doi:10.1364/JOSAB.31.000551
[13] G. P. Agrawal, Nonlinear Fiber Optics, 4th edn., Academic Press, New York (2007)



