定义
用于量化介质克尔非线性的参数。
当高强度光通过介质传播时,这会导致非线性效应。 其中最简单的是克尔效应,它可以描述为折射率与光学强度成比例的变化(通常是增加) I
具有非线性折射率(简称:非线性折射率)) n2。该数量的单位是 m2/W(或cm2/W ) 在 SI 系统中,但在较旧的文献中发现n2以 ESU 为单位的值。 对于此类单位的转换,公式

可以使用,其中n是折射率。
非线性指数由χ(3) 材料的非线性,可以计算为:
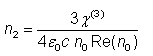
这表明高非线性指数通常是由高χ(3)值,但如果折射率变得非常小,例如由于声子共振效应或光子超材料,也可以增加。 这两个涉及的量可能在某种程度上取决于波长。
通常,非线性指数是针对线性偏振光测量的。 对于非双折射介质中的圆偏振光,克尔效应弱三分之一。
其他并发症
在非常高的光学强度下,上述非线性折射率变化方程可能需要更高阶的校正。 例如,可能有一个与指数平方成正比的项,具有负系数,以便克尔效应饱和。
除了克尔效应(一种纯电子非线性)之外,电致伸缩还可以显著影响非线性指数的值[9,10]。 在这里,光的电场引起密度变化(声波),其本身通过光弹性效应影响折射率。 然而,这种机制涉及明显的时间延迟,因此仅与相对较慢的功率调制有关,而与超短脉冲无关。 在光纤中,低(兆赫兹)频率下电致伸缩的贡献通常是克尔效应的10-20%,但可能在很大程度上取决于材料。
非线性折射率的值
对于透明晶体和玻璃,n2通常为 10−16 cm2/W 至 10−14 cm2/W 。熔融石英,例如用于二氧化硅纤维,具有特别低的非线性指数,为2.7 · 10−16 cm2/W 波长约为 1.5 μm,而一些硫族化物玻璃表现出数百倍的值。
半导体材料也具有非常高的非线性指数值。 已经表明,非线性指数与带隙能量的反四次方成正比,但也取决于测试波长与带隙的接近程度[5]。 非线性也可能是负的(自散焦非线性),特别是对于高于带隙能量≈70%的光子能量。
| 材料 | 非线性指数 | 参考 |
|---|---|---|
| 空气 | 1.22 ·10−22 m2/W 在 308 纳米处,1 个大气压 |
[2] |
| 熔融石英 | 2.19 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 蓝宝石 | 2.8 ·10−20 m2/W 在 1550 nm 处 |
[12] |
| 钇铝石榴石(Y3Al5O12) | 6.13 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 钒酸钇(YVO4), no | 15.6 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 钒酸钇(YVO4), ne | 14.9 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 方解石(CaCO3), no | 3.22 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 方解石(CaCO3), ne | 2.12 ·10−20 m2/W 在 1030 nm 处 |
[17] |
| 氟化钙(CaF2) | 1.71 ·10−20 m2/W 在 1030 nm 处 |
[17] |
各种材料的非线性指数值。请注意,对于双折射材料,这些值与偏振有关。请注意,10−20 m2/W = 10−16 cm2/W 。
具有高非线性指数的材料通常具有较小的带隙能量,因此也经常表现出强烈的双光子吸收(TPA)。 对于某些应用,例如电信系统中的信道转换,这是有害的,并且品质因数例如n2 / β(其中β是TPA系数)可用于比较不同的材料。
对于折射率接近零的材料,也会产生非常高的非线性折射率。 例如,氧化铟锡(ITO)表现出巨大的n21250 nm 附近波长区域的值 [15]。 在1300nm区域的铝掺杂氧化锌(AZO)中也观察到了类似的效应[16]。 请注意,这种极强的非线性仍然可以表现出超快的响应,即在亚皮秒时间尺度上。 例如,它们可能对非线性信号处理有用。
注意,偶数空气也表现出一些克尔非线性,非线性指数在5 · 10−19 cm2/W 表示可见光和大气压。
非线性指数的测量
大块样品非线性指数的测量通常使用z扫描技术完成,该技术基于通过Kerr透镜的自聚焦。
折射率非常高的情况的另一种可能性是使用泵浦-探头测量:脉冲泵浦光束会引起随时间变化的相位变化,从而导致光谱变化,并且可以测量这些变化[18]。
光纤的非线性可以通过测量自相位调制产生的光谱展宽来量化。 但请注意,偏振状态可能会在非保偏光纤中打乱,这可能会影响结果。 此外,结果是对纤芯和包层的材料特性的一种平均值。
参考文献
[1] M. J. Weber, D. Milam. and W. L. Smith, “Nonlinear refractive index of glasses and crystals”, Opt. Eng. 17, 463 (1978), doi:10.1117/12.7972266
[2] Y. Shimoji et al., “Direct measurement of the nonlinear refractive index of air”, J. Opt. Soc. Am. B 6 (11), 1994 (1989), doi:10.1364/JOSAB.6.001994
[3] M. Sheik-Bahae et al., “Sensitive measurement of optical nonlinearities using a single beam”, IEEE J. Quantum Electron. 26 (4), 760 (1990), doi:10.1109/3.53394
[4] D. W. Hall et al., “Nonlinear optical susceptibilities of high-index glasses”, App. Phys. Lett. 54 (14), 1293 (1989), doi:10.1063/1.100697
[5] M. Sheik-Bahae et al., “Dispersion and band-gap scaling of the electronic Kerr effect in solids associated with two-photon absorption”, Phys. Rev. Lett. 65 (1), 96 (1990), doi:10.1103/PhysRevLett.65.96
[6] K. S. Kim et al., “Measurement of the nonlinear index of silica-core and dispersion-shifted fibers”, Opt. Lett. 19 (4), 257 (1994), doi:10.1364/OL.19.000257
[7] T. Kato et al., “Measurement of the nonlinear refractive index in optical fiber by the cross-phase-modulation method with depolarized pump light”, Opt. Lett. 20 (9), 988 (1995), doi:10.1364/OL.20.000988
[8] T. Kato, Y. Suetsugu and M. Nishimura, “Estimation of nonlinear refractive index in various silica-based glasses for optical fibers”, Opt. Lett. 20 (22), 2279 (1995), doi:10.1364/OL.20.002279
[9] E. L. Buckland and R. W. Boyd, “Electrostrictive contribution to the intensity-dependent refractive index of optical fibers”, Opt. Lett. 21 (15), 1117 (1996), doi:10.1364/OL.21.001117
[10] E. L. Buckland and R. W. Boyd, “Measurement of the frequency response of the electrostrictive nonlinearity in optical fibers”, Opt. Lett. 22 (10), 676 (1997), doi:10.1364/OL.22.000676
[11] I. P. Nikolakakos et al., “Broadband characterization of the nonlinear optical properties of common reference materials”, IEEE Sel. Top. Quantum Electron. 10 (5), 1164 (2004), doi:10.1109/JSTQE.2004.836007
[12] A. Major et al., “Dispersion of the nonlinear refractive index in sapphire”, Opt. Lett. 29 (6), 602 (2004), doi:10.1364/OL.29.000602
[13] Shahraam Afshar V. et al., “Small core optical waveguides are more nonlinear than expected: experimental confirmation”, Opt. Lett. 34 (22), 3577 (2009), doi:10.1364/OL.34.003577
[14] I. Dancus et al., “Single shot interferometric method for measuring the nonlinear refractive index”, Opt. Express 21 (25), 31303 (2013), doi:10.1364/OE.21.031303
[15] M. Z. Alam, I. De Leon and R. W. Boyd, “Large optical nonlinearity of indium tin oxide in its epsilon-near-zero region”, Science 352 (6287), 795 (2016), doi:10.1126/science.aae0330
[16] L. Caspani et al., “Enhanced nonlinear refractive index in ε-near-zero materials”, Phys. Rev. Lett. 116, 233901 (2016), doi:10.1103/PhysRevLett.116.233901
[17] P. Kabacinski et al., “Nonlinear refractive index measurement by SPM-induced phase regression”, Opt. Express 27 (8), 11018 (2019), doi:10.1364/OE.27.011018
[18] Y. Zhou et al., “Broadband frequency translation through time refraction in an epsilon-near-zero material”, Nature Communications 11, 2180 (2020), doi:10.1038/s41467-020-15682-2
[19] G. N. Patwardhan et al., “Nonlinear refractive index of solids in mid-infrared”, Opt. Lett. 46 (8), 1824 (2021), doi:10.1364/OL.421469



