定义
使用描述超短脉冲传播的物理模型,例如在激光器或光纤中。
在透明光学介质中传播时,超短光脉冲的性质会发生复杂的变化。 影响脉冲的典型物理效应是:
- 色散会导致色散脉冲展宽,但也会导致脉冲压缩、产生啁啾等。
- 在高峰值功率下,各种非线性都可能变得相关。 例如,克尔效应可以引起自相位调制,拉曼散射可能会在脉冲频谱内诱导拉曼增益(拉曼自频移)。
- 光增益和损耗可以改变脉冲能量和光谱形状。
- 空间属性可能会由于线性效应(例如衍射和波导)而发生变化,也可以由于非线性效应(例如自聚焦)而发生变化。 在高度非线性的相互作用中,可能会发生灯丝。
当然,不同的效果可以同时起作用,并且经常以令人惊讶的方式相互作用。 例如,色散和克尔非线性会导致孤子效应。
脉冲传播效应的相关性
上述脉冲传播效应在各种情况下都很重要。 一些例子是:
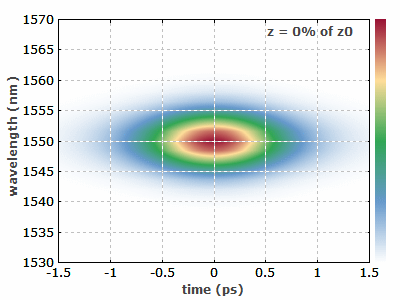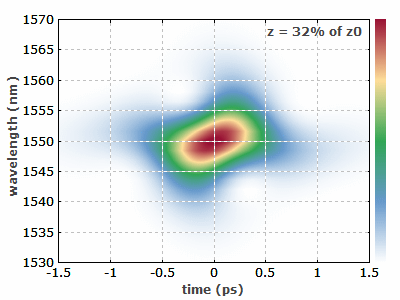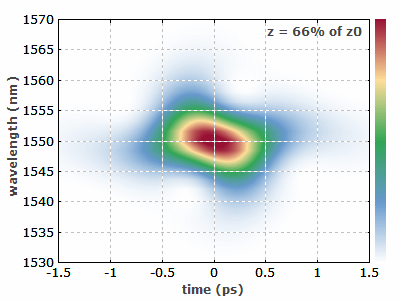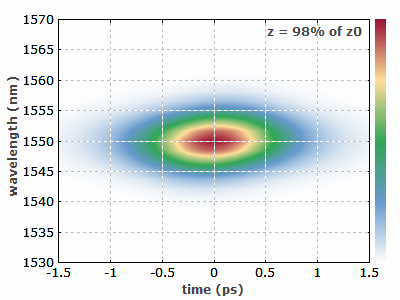
图1:这个动画频谱图显示了三阶孤子如何在光纤中演化。高阶孤子表现出更复杂的行为。图像是用RP Propulse软件生成的。
- 超短脉冲在锁模激光器中的传播细节决定了稳态脉冲特性,如脉冲持续时间、带宽和线性调频,以及脉冲产生、多脉冲等的稳定性。
- 光纤中的传播与脉冲放大、脉冲压缩和超连续体生成以及光纤通信有关。
- 超短脉冲的非线性频率转换会导致脉冲形状的复杂变化。 除了非线性相互作用之外,还可能受到时间空间走开和色散展宽等效应的影响。
脉冲传播建模技术
根据情况,需要不同类型的物理建模技术。 下面简要介绍了一些最重要的问题:
- Haus Master方程是一种分析工具,主要用于计算锁模激光器中获得的稳态脉冲特性。 它可以看作是非线性薛定谔方程的推广。
- 孤子扰动理论描述了孤子脉冲的传播,孤子脉冲可能受到增益或损耗、光谱滤波等的影响。 许多动力学方程描述了在各种效应影响下孤子基本参数的演变。 此外,还包括所谓的连续统,即孤子可以与之相互作用的时间宽背景辐射。 例如,可以使用孤子扰动理论来描述凯利边带的产生。
- 基于脉冲复杂电场的二阶矩的模型[5]也可以大大减少动态变量的数量。 但是,只有在脉冲形状保持相对简单的情况下,它们才适用。 困难在于,具有合理精度的参数区域在哪里结束并不总是很明显。 随着计算机能力的提高,计算速度明显更快的优势(与完整的数值模拟相比)变得不那么重要了。
- 数值技术可用于在更一般的情况下模拟脉冲传播。例如,适用于锁模激光器的简单方法描述了在时域或频域中具有复杂振幅阵列的短脉冲。 线性效应(如色散)在频域中很容易处理,而非线性相互作用通常(但并非总是)在时域中处理得更方便。 根据需要,可以使用快速傅里叶变换算法(FFT技术)在两个域之间切换。
- 一种特殊情况是对称分步傅里叶法,特别用于光纤中的脉冲传播[9]。 对应于短纤维片的(弱)色散和非线性效应交替应用。 与有限纵向步长相关的数值误差可以通过特殊的对称技术最小化,该技术允许更高的精度,而不会过度增加计算时间。 自动步长控制对于计算效率非常重要。
- 更精细的技术也考虑到了横向空间变化。 例如,它们可用于研究克尔镜头模式锁定或灯丝现象。
- 对于多模波导中的传播,将光场描述为传播模式的叠加通常是有利的,可以通过非线性等方式进行耦合。
通过应用统计技术,脉冲传播模型也可用于研究噪声现象[7]。
参考文献
[1] P. V. Mamyshev and S. V. Chernikov, “Ultrashort-pulse propagation in optical fibers”, Opt. Lett. 15 (19), 1076 (1990), doi:10.1364/OL.15.001076
[2] G. P. Agrawal, “Optical pulse propagation in doped fiber amplifiers”, Phys. Rev. A 44 (11), 7493 (1991), doi:10.1103/PhysRevA.44.7493
[3] H. A. Haus et al., “Structures for additive pulse mode locking”, J. Opt. Soc. Am. B 8 (10), 2068 (1991), doi:10.1364/JOSAB.8.002068
[4] P. L. François, “Nonlinear propagation of ultrashort pulses in optical fibers: total field formulation in the frequency domain”, J. Opt. Soc. Am. B 8 (2), 276 (1991), doi:10.1364/JOSAB.8.000276
[5] M. Potasek et al., “Analytic and numerical study of pulse broadening in nonlinear dispersive fibers”, J. Opt. Soc. Am. B 3 (2), 205 (1992), doi:10.1364/JOSAB.3.000205
[6] D. Marcuse, “RMS width of pulses in nonlinear dispersive fibers”, IEEE J. Lightwave Technol. 10 (1), 17 (1992), doi:10.1109/50.108730
[7] R. Paschotta, “Noise of mode-locked lasers. Part I: numerical model”, Appl. Phys. B 79, 153 (2004); R. Paschotta, “Noise of mode-locked lasers. Part II: timing jitter and other fluctuations”, Appl. Phys. B 79, 163 (2004), doi:10.1007/s00340-004-1548-9
[8] B. Burgoyne et al., “Nonlinear pulse propagation in optical fibers using second order moments”, Opt. Express 15 (16), 10075 (2007), doi:10.1364/OE.15.010075
[9] G. P. Agrawal, Nonlinear Fiber Optics, 4th edn., Academic Press, New York (2007)
[10] R. Paschotta, tutorial on "Passive Fiber Optics"
[11] R. Paschotta, tutorial on "Passive Fiber Optics", Part 12: Ultrashort Pulses and Signals in Fibers
[12] R. Paschotta, tutorial on "Modeling of Fiber Amplifiers and Lasers", part 7



