定义
光学场产生准直流非线性偏振的非线性过程。
当光在具有χ(2) 非线性,由此产生的非线性极化具有准直流分量,即具有非零平均值。 这是因为光学非线性不仅可以产生与所涉及的光学频率的和和差(→和差频生成)相关的非线性偏振的频率分量,而且会产生频率是某些光学频率与自身的差值的分量,即零频率。
对于具有近似恒定或缓慢变化的光束,发生的准DC(低频)非线性偏振通常没有明显的影响。 然而,在超短脉冲的情况下,准直流分量的强度迅速上升和下降,这导致具有宽频谱的电磁单周期脉冲的辐射,范围大致从零频率到某个最大值,其中相位匹配情况下的总带宽基本上由脉冲持续时间的倒数决定. 例如,对于持续时间为100飞秒的光脉冲,产生的辐射脉冲的频率分量超过10 THz(→太赫兹辐射),也可以被视为远红外辐射。
可以证明,负责光学整流的非线性张量与材料的电光张量直接相关。 因此,在文献中,人们经常指定材料的有效电光系数(以pm/V为单位),而不是相应的χ(2)组件,具有相同的单位但不同的大小。 (转换因子涉及折射率。)
光学整流的各个方面都不同于其他非线性转换过程,例如倍频:
- 由于产生的辐射频率低,对于给定强度的非线性极化,辐射非常弱。 实现的转换效率通常非常低 - 在最好的情况下,只有百分之几。
- 生成的太赫兹带宽通常与泵浦脉冲带宽相当,但与平均太赫兹频率相比,该带宽非常大。 例如,这意味着辐射效率和衍射效应的强度在脉冲光谱内变化很大。
- 所使用的晶体通常在太赫兹范围内表现出大量的吸收,而在光学域中的寄生吸收通常非常弱。
- 在某些情况下,太赫兹波的折射率远大于光束的折射率,这极大地限制了相位匹配方案的选择。
材料和相位匹配方案
非常不同的材料可用于产生具有光学整流的太赫兹波:
- 传统的无机非线性晶体材料,如铌酸锂(LiNbO3)和钽酸锂(LiTaO3)被广泛使用。 它们相对坚固,并且易于获得大尺寸。
- 在某些情况下,使用有机晶体,如DAST = 4-二甲氨基-N-甲基二苯唑对甲苯磺酸盐,OH1 = 2-(3-(4-羟基苯乙烯基)-5,5-二甲基环己基-2-亚烯基)丙二腈和DSTMS = 4-N,N-二甲氨基-4'-N'-甲基-二苯唑鎓2,4,6-三甲基苯磺酸盐[8],其通常表现出非常强的非线性(电光系数>100 pm/V,比典型的无机晶体高两个数量级)。 这允许高效的太赫兹转换,即使对于中等的光学通量也是如此。
- 一些有机材料也可以以聚合物(而不是单晶)形式使用;所需的χ(2)可以通过电场极化产生[5]。
- 各种半导体也是合适的,例如砷化镓(GaAs),磷化镓(GaP),碲化镉(CdTe)和碲化锌(ZnTe)。 使用的非线互作用不一定基于χ(2)体非线性,但也可能是静态表面损耗场和材料χ(3)非线性,特别是对于高脉冲通量。
在任何情况下,只有实现非线性相互作用的相位匹配,或者至少晶体长度内的相位失配不太大,才能实现实质性的功率转换效率。 有不同的相位匹配方案,可以应用于不同的晶体材料。 例如,对于磷化镓(GaP)中1μm光谱区域的光脉冲,可以实现简单的共线相位匹配。 其他晶体材料允许其他光学波长的相位匹配,例如1.3μm的砷化镓;相位匹配带宽相当大,因此在合理的晶体长度下,甚至可以在1.5μm区域工作。
在其他材料中,如铌酸锂(LiNbO3),太赫兹波的折射率对于共线相位匹配来说太大了;在这里,可以采用切伦科夫相位匹配方案,其中产生的辐射在侧面耦合(例如,将硅棱镜连接到非线性晶体的侧面,以抑制晶体 - 空气边界处的全内反射)。
在某些情况下,使用角度色散(即倾斜脉冲前沿)[10,16,27],在高脉冲能量的状态下实现相对较高的转换效率。 在其他情况下,在周期性极化晶体中采用准相位匹配[17];即使是导致窄带太赫兹发射的向后发射,也不需要过小的极点周期[7,23],因为太赫兹辐射的波数很小。
即使在空气等气体中,当等离子体由红外束与其二次谐波叠加产生等离子体时,也可以通过飞秒脉冲的光学整流产生太赫兹[20]。 对所涉及的波进行仔细的相位控制对于高转换效率是必要的。 与晶体中的光学整流相比,发射带宽通常更高,可以获得更高的脉冲能量。
太赫兹脉冲参数的依赖关系
对于给定的脉冲持续时间和时间形状,辐射太赫兹能量与光脉冲能量的平方和有效非线性系数的平方成正比deff 这意味着功率转换效率与脉冲能量成正比。 (在具有大量双光子吸收或其他饱和效应的情况下,该定律不成立。
对于给定的脉冲能量,生成的太赫兹脉冲的能量与反脉冲持续时间的五次方成正比(至少在简单情况下)。 这可以理解如下:
由于各种原因,较短的泵浦脉冲允许更高的太赫兹脉冲能量。
- 辐射幅度与电荷加速度有关,即与极化的二次导数有关,辐射强度与振幅的平方成正比。 因此,如果给定一定的振荡幅度,正弦振荡偶极子辐射的功率与振荡频率的第四次方成正比。
- 因此,如果峰值极化恒定,则每个振荡周期辐射的能量与脉冲持续时间的反三次方成正比。 单脉冲光整流引起的辐射也是如此,可以认为这是非线性偏振的单次振荡周期。
- 辐射能量也与非线性偏振的振荡幅度的平方成正比,而非线性偏振振本身与电场强度的平方成正比,从而与光学峰值功率成正比,因此与给定脉冲能量的脉冲持续时间成反比。
总之,当脉冲持续时间减少而脉冲能量保持恒定时,辐射太赫兹能量会非常强烈地增加 - 这只是由于当时更高的峰值光学强度。 如上所述,较短的脉冲也意味着太赫兹脉冲的带宽更大。 图3显示了两种情况下的太赫兹光谱。
下图还说明了脉冲持续时间的影响,使用了一个非常简化的模型,该模型忽略了不完美的相位匹配、频率相关的衍射和吸收等细节。 尽管两种情况下的峰值功率相同,但对于较短的脉冲,产生的太赫兹电场要强得多,因为非线性极化的二次导数要强得多。

图1:100-fs 泵浦脉冲的光强度和太赫兹电场。

图2:200-fs泵浦脉冲的光强度和太赫兹电场。
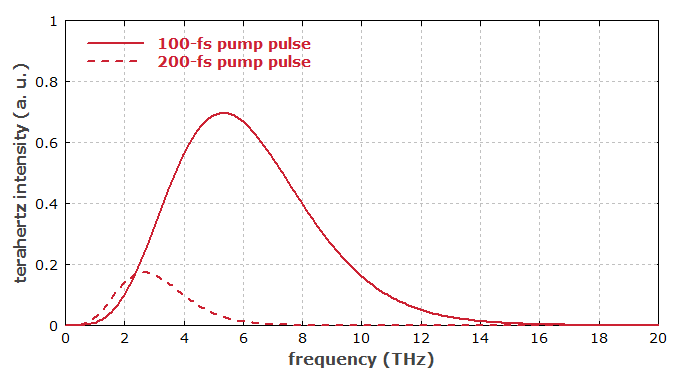
图3:不同脉冲持续时间产生的太赫兹辐射光谱。
由于太赫兹辐射波长较长,会产生强烈的衍射效应。
在简单的情况下,所用非线性晶体的较长长度可以按晶体长度的平方成比例地增加获得的太赫兹脉冲能量 - 例如,类似于倍频的情况。 然而,即使实现了完美的相匹配,各种有害效应也会降低增加晶体长度的有益效应。 特别是,由于太赫兹辐射的波长较长(通常为数百微米量级),存在强烈的衍射效应:即使激光束在整个晶体中可以具有近似恒定的光束半径,开始时产生的太赫兹辐射也可以在到达晶体末端之前横向膨胀,这不仅会导致更大的输出光束, 但也降低了转换效率(类似于其他非线互中的空间走开)。 此外,晶体材料中的太赫兹辐射可能会有大量吸收。 当所涉及的频率达到材料的声子频率时,情况尤其如此。
由于已经提到的衍射效应,激光束的更紧密聚焦也仅在有限的程度上有所帮助。 高激光脉冲能量允许人们仅使用激光束的温和聚焦(同时保持高强度),因此衍射效应较弱。
非线性转换过程的详细计算通常需要一个复杂的数值模型,描述空间和时间的依赖关系。 这样的模型可以考虑各种影响:
通过整流对非线性转换进行精确计算通常需要相当复杂的数值模型。
- 太赫兹辐射的自由载流子吸收和晶体材料的声子共振会降低获得的输出功率。 (在某些情况下,在生成的光谱中可以看到强烈的吸收线。
- 通常需要考虑太赫兹波的波长相关衍射,可能还需要考虑光泵浦光束的衍射。
- 在大量功率转换的情况下,可能会发生泵耗尽效应。 此外,双光子吸收可能会在高强度水平下衰减泵浦波。
- 群速度色散可能是相关的,也可能是角色散和群速度不匹配。
- 在某些材料中,如LiNbO3,极化子共振可以增强有效的非线性度[24]。
参考文献
[1] M. Bass et al., “Optical rectification”, Phys. Rev. Lett. 9 (11), 446 (1962), doi:10.1103/PhysRevLett.9.446
[2] K. H. Yang, P. L. Richards and Y. R. Shen, “Generation of far-infrared radiation by picosecond light pulses in LiNbO3”, Appl. Phys. Lett. 19 (9), 320 (1971), doi:10.1063/1.1653935
[3] D. H. Auston et al., “Cherenkov radiation from femtosecond optical pulses in electro-optic Media”, Phys. Rev. Lett. 53 (16), 1555 (1984), doi:10.1103/PhysRevLett.53.1555
[4] J. B. Khurgin, “Optical rectification and terahertz emission in semiconductors excited above the band gap”, J. Opt. Soc. Am. B 11 (12), 2492 (1994), doi:10.1364/JOSAB.11.002492
[5] A. Nahata et al., “Generation of terahertz radiation from a poled polymer”, Appl. Phys. Lett. 67 (10), 1358 (1995), doi:10.1063/1.115550
[6] A. Nashata and T. F. Heinz, “Generation of subpicosecond electrical pulses by optical rectification”, Opt. Lett. 23 (11), 867 (1998), doi:10.1364/OL.23.000867
[7] Y. J. Ding and J. B. Khurgin, “A new scheme for efficient generation of coherent and incoherent submillimeter to THz waves in periodically-poled lithium niobate”, Opt. Commun. 148, 105 (1998), doi:10.1016/S0030-4018(97)00611-1
[8] P. Y. Han et al., “Use of the organic crystal DAST for terahertz beam applications”, Opt. Lett. 25 (9), 675 (2000), doi:10.1364/OL.25.000675
[9] R. Spreiter, C. Bosshard and P. Günter, “Boundary conditions for optical rectification and application to degenerate four-wave mixing in a novel geometry”, J. Opt. Soc. Am. B 18 (9), 1311 (2001), doi:10.1364/JOSAB.18.001311
[10] J. Hebling et al., “Velocity matching by pulse front tilting for large area THz pulse generation”, Opt. Express 10 (21), 1161 (2002), doi:10.1364/OE.10.001161
[11] T. Taniuch and H. Nakanishi, “Collinear phase-matched terahertz-wave generation in GaP crystal using a dual-wavelength optical parametric oscillator”, J. Appl. Phys. 95 (12), 7588 (2004), doi:10.1063/1.1751238
[12] Y. J. Ding, “Quasi-single-cycle THz pulses based on broadband phase-matched difference-frequency generation in second-order nonlinear medium: high output powers and conversion efficiencies”, J. Sel. Top. Quantum Electron. 10, 1171 (2004), doi:10.1109/CLEO.2005.202156
[13] I. Tomita et al., “Terahertz-wave generation from quasi-phase-matched GaP for 1.55 μm pumping”, Appl. Phys. Lett. 88 (7), 071118 (2006), doi:10.1063/1.2174832
[14] A. Schneider et al., “Generation of terahertz pulses through optical rectification in organic DAST crystals: theory and experiment”, J. Opt. Soc. Am. B 23 (9), 1822 (2006), doi:10.1364/JOSAB.23.001822
[15] G. Chang et al., “Power scalable compact THz system based on an ultrafast Yb-doped fiber amplifier”, Opt. Express 14 (17), 7909 (2006), doi:10.1364/OE.14.007909
[16] K. L. Yeh et al., “Generation of 10 μJ ultrashort terahertz pulses by optical rectification”, Appl. Phys. Lett. 90 (17), 171121 (2007), doi:10.1063/1.2734374
[17] K. L. Vodopyanov, “Optical THz-wave generation with periodically-inverted GaAs”, Laser & Photonics Reviews 2 (1-2), 11 (2008), doi:10.1002/lpor.200710028
[18] A. G. Stepanov et al., “Generation of 30 μJ single-cycle terahertz pulses at 100 Hz repetition rate by optical rectification”, Opt. Lett. 33 (21), 2497 (2008), doi:10.1364/OL.33.002497
[19] S. Xu et al., “Broadband terahertz generation through intracavity nonlinear optical rectification”, Opt. Express 18 (22), 22625 (2010), doi:10.1364/OE.18.022625
[20] J. Dai et a l., “Terahertz wave air photonics: terahertz wave generation and detection with laser-induced gas plasma”, IEEE J. Sel. Top. Quantum. Electron. 17 (1), 183 (2011), doi:10.1109/JSTQE.2010.2047007
[21] H. Hirori et al., “Single-cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO3”, Appl. Phys. Lett. 98 (9), 091106 (2011), doi:10.1063/1.3560062
[22] J. A. Fülöp et al., “Towards generation of mJ-level ultrashort THz pulses by optical rectification”, Opt. Express 19 (16), 15090 (2011), doi:10.1364/OE.19.015090
[23] R. Chen et al., “Generation of high-frequency terahertz waves in periodically poled LiNbO3 based on backward parametric interaction”, Appl. Phys. Lett. 101, 111101 (2012), doi:10.1063/1.4751843
[24] X. Lin, L. Wang, and Y. J. Ding, “Efficient generation of far-infrared radiation in the vicinity of polariton resonance of lithium niobate”, Opt. Lett. 37 (17), 3687 (2012), doi:10.1364/OL.37.003687
[25] V. Vicario et al., “Generation of 0.9-mJ THz pulses in DSTMS pumped by a Cr:Mg2SiO4 laser”, Opt. Lett. 39 (23), 6632 (2014), doi:10.1364/OL.39.006632
[26] W. Schneider et al., “800-fs, 330-μJ pulses from a 100-W regenerative Yb:YAG thin-disk amplifier at 300 kHz and THz generation in LiNbO3”, Opt. Lett. 39 (23), 6604 (2014), doi:10.1364/OL.39.006604
[27] K. Ravi et al., “Theory of terahertz generation by optical rectification using tilted-pulse-fronts”, Opt. Express 23 (4), 5253 (2015), doi:10.1364/OE.23.005253
[28] S. Carbajo et al., “Efficient narrowband terahertz generation in cryogenically cooled periodically poled lithium niobate”, Opt. Lett. 40 (24), 5762 (2015), doi:10.1364/OL.40.005762
[29] F. Meyer et al., “Optical rectification of a 100-W average power mode-locked thin-disk oscillator”, Opt. Lett. 43 (24), 5909 (2018), doi:10.1364/OL.43.005909
[30] M. Hamrouni et al., “Intra-oscillator broadband THz generation in a compact ultrafast diode-pumped solid-state laser”, Opt. Express 29 (15), 23729 (2021), doi:10.1364/OE.426750
[31] I. Wilke and S. Sengupta, “Nonlinear Optical Techniques for Terahertz Pulse Generation and Detection – Optical Rectification and Electrooptic Sampling”, chapter 2 in Terahertz Spectroscopy: Principles and Applications, edited by S. L. Dexheimer, Optical Science and Engineering Vol. 131, 41, CRC Press (2007)



