定义
由于周期性光学纳米结构而具有特殊光学性质的介质。
光子晶体是包含周期性纳米结构的光学介质 - 通常是折射率的周期性变化,其中发生的周期是光学波长的数量级。 虽然在某些情况下存在相当大的折射率对比度,例如在玻璃或半导体与空气之间,但在其他情况下会出现低得多的折射率对比度。 一些特别显着的光子晶体特性 - 例如完全光子带隙 - 主要出现在具有大折射率对比度的情况下,这就是为什么一些作者建议要求光子晶体具有较大的折射率对比度。
这一研究领域在基础科学和实际应用方面都非常重要,由Eli Yablonovitch [1](他也引入了光子晶体一词)和Sajeev John[2]开创,随后还有许多其他研究人员。 对一维周期结构(多层介电堆栈→作为布拉格镜的介电涂层)的早期研究已经由瑞利勋爵在1887年进行。 虽然光子晶体主要在现代技术领域处理,但在自然界中也观察到光子晶体结构,例如某些矿物(例如蛋白石)和生物体,例如在蝴蝶翅膀中。
光子晶体和光子超材料之间有明显的相似之处:后者通常还涉及具有光学效应的结构的周期性排列。 然而,光子超材料具有亚波长尺度的结构,使得这些结构在光场中看起来是均匀的,并且由此产生的显着性质不是用光子带结构来解释的,而是基本上用折射率的异常值来解释的。
与晶体介质中的电子类比
电子态和布洛赫函数
在20世纪初,固体的许多基本性质,如它们变化广泛的导电性和导热性,透光率或吸收率仍然没有得到理解。 然后通过考虑周期性静电势中电子的波函数取得了实质性进展,就像晶体材料中原子核的周期性排列所产生的那样。
虽然最初必须预期非常强烈的电势变化应该导致电子在这种结构中的强散射,但发现这种周期性结构表现出可以用布洛赫函数描述的电子的特征态。 布洛赫函数的形式为
其中k是可变波矢量,确定长距离的相演变,u函数具有电势的周期性。 布洛赫波是一种驻波——请注意,由u函数确定的强度分布在空间中保持固定。 不同的解用离散指数j区分。 波矢量原则上可以任意选择,但仅考虑第一布里渊区内的波矢量就足够了;该区域之外的向量只会导致相同的解决方案。 使用合适的数学方法,对于给定的势,可以计算出得到的布洛赫函数,并且对于每个电位,可以计算出相应的电子能量(作为特征值)。 考虑到一个无限大的晶体,人们可以获得布洛赫函数和能量值的连续统一体。
对于指数j的每个值,波矢量的变化导致一定范围的电子能量,称为能带。 这些能带通常彼此重叠,导致可能的电子能量的宽连续范围,但在某些情况下会发生带隙,即对于任何可用的特征态都不会发生的电子能量范围。
每个布洛赫态都是完全离域的,这意味着处于这种状态的电子不对应于某个原子核,但原则上可以在整个晶体的任何地方找到。 局部电子状态只出现在某些晶格缺陷上。
原则上,电子将永远保持其本征态,除非额外的效应导致状态之间的转换 - 无论是在带内还是跨能带。 例如自发发射,光的吸收和受激发射,以及与声子,其他电子或晶格缺陷的相互作用。
如果没有这种额外的耦合效应,尽管原子核处有很强的散射,但计算出的状态是特征态。 人们认为特征态是一组平面波的叠加态,它们朝着非常不同的方向移动,因此尽管它们之间存在很强的耦合,但它们的整体模式仍然是静止的。
电子本征态的最终结构与泡利原理相结合具有各种重要后果:
- 光的吸收(在线性范围内,即没有过多的光学强度)只有在光子能量适合将填充初始状态与非填充的高能态连接时才有可能。 此外,对所涉及的波矢量存在限制,换句话说,基于动量守恒原理:初始和最终能级必须具有非常相似的波矢量,因为相关能量范围内(例如红外光、可见光或紫外线)中光子的波矢量相对较小。
- 类似的限制适用于自发和受激发射,它将电子带到低洼状态。
- 完全填充的带不能促进电传导,因为不可能重新分布水平群体。 部分填充的带,特别是在金属中,有助于电传导和热传导。 原则上,导热率和导电性可以非常高,但可以通过引起散射的晶格缺陷而大大降低。
绝缘体(电介质)、半导体和金属的许多基本特性可以根据它们的电子能带结构来解释。
周期介质中的光子状态
在光子学中,人们处理光的传播,即电磁波。 在周期性光子纳米结构的情况下,由周期性变化的折射率n或介电常数ε描述,可以在这样的条件下建立波动方程,其中平面波当然不是特征解(如在均匀介质中)。
就像在电子的固态物理学中一样,人们可以证明再次存在布洛赫波,但这次使用描述复杂电场振幅的函数而不是电子波函数。 但是,在各个方面,情况有所不同:
电子和光子状态之间的类比到目前为止并不完美;然而,许多见解可以从一个领域转移到另一个领域。
- 虽然电子波函数是标量函数,但电场是矢量场,导致不同极化状态的可能性。
- 另一方面,虽然由于忽略了电子 - 电子相互作用,对具有能带结构的电子状态的描述有些不准确,但这种复杂性不会发生在光子晶体中。
- 因为电子有质量而光子没有,所以它们在自由空间中的色散关系是不同的。
- 光子是玻色子,而电子是费米子,这种差异对状态的可能占领具有深远的影响。
尽管如此,固态物理学的大量见解可以以非常相似的形式用于光子晶体的分析:
- 有布洛赫函数描述第一布里渊区域内波矢量的可能特征解,相应的特征值是光学频率。 当然,第一个布里渊区的尺寸比电子态的尺寸小约三个数量级,因为调制周期要长得多。
光子带隙对于许多应用至关重要,但也有利用带内特性的情况。
- 再次可能存在带隙(这里称为光子带隙或光子带隙,PBG,或有时不太精确的阻带),其中光学频段不重叠。 对于这种带隙内的频率,光不能在材料中传播 - 从某种意义上说,没有合适的布洛赫态,而只有振幅指数衰减的解,这意味着可观的光振幅只能在有限的距离内发生。 因此,具有这种频率的入射光必须被光子晶体反射。 对于完整的光子带隙,甚至可以获得全向反射。
- 在波段内,传播光具有特殊的特性。 它总是具有在不同方向上传播的组件,这些组件彼此耦合。 这也对光能的传输和群速度产生了深远的影响。 在这种光子带结构的那些部分,轮廓变得非常平坦,可能会出现远低于普通光速的群速度。 由于可能的k值与频率有很大的依赖性,因此也可能发生高度异常的色散。
- 在光子晶体和普通光学材料之间的边界上可能发生进一步的特殊效应。 例如,可能存在负折射和超棱镜效应。
在光子带隙的存在是必不可少的情况下,这种材料通常也称为光子带隙材料。 它们有时也被称为光子绝缘体或光子半导体,因为电绝缘体和半导体是电子能带结构表现出带隙的那些。
人们可能想知道原子尺度上的周期性(对于晶体材料)是否也可以发挥作用。 然而,这个长度尺度太短了,与光无关,波长尺度要长得多。
一维、二维和三维光子晶体
光子晶体可以在不同的维度上实现,这将在以下各节中讨论。
一维光子晶体
一维周期性结构是否应该被定性为光子晶体是有争议的;先驱雅布洛诺维奇拒绝了这一点。 然而,无论如何,它们都是分析光子晶体基本性质的良好起点,而不会在更高维度上发挥作用。

图1:一维光子晶体结构,包含具有不同折射率的两种材料的层(不需要具有相同的厚度)。
如上所述,瑞利勋爵在19世纪后期就已经考虑了介电多层层堆栈形式的一维周期结构(图1)。 如今,它们通常用作介电镜,在最简单的情况下,采用布拉格镜的设计。 人们经常只是忽略额外的空间维度,只考虑传播到完全相反方向的光,通过周期性折射率调制相互耦合。
数学上最简单的情况实际上发生在介电常数的正弦(而不是矩形)调制中,尽管对于技术应用,层压材料的逐步调制更为常见 - 通过使用两种不同材料的层来实现,而不是不太常见的Rugate滤波器中使用的连续调制. 可以很容易地证明,对于介电常数调制幅度的消失,可以获得没有任何带隙的简单带隙结构,但是随着调制强度的增加,尺寸增加的带隙就会出现。 在这样的频率区域中,人们在一个方向上获得电场振幅的指数衰减(忽略短长度尺度上的调制),这意味着光不能在很长的距离内传播到这样的结构中。
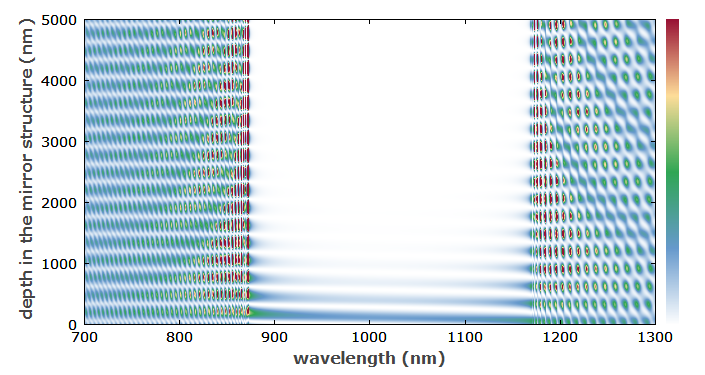
图2: 用RP Coating软件计算了含有100层非晶TiO2和SiO2的介质布拉格镜的场穿透率
对多层结构的简单计算已经可以很好地了解由此产生的光子带隙。
通过计算具有100层对的布拉格镜的光学特性,人们已经可以在一定程度上探索无限周期结构的光子带隙的近似性质,从零到无穷大在z方向上延伸。 图2显示了这种结构的现场穿透。 在大约 875 nm 至 1165 nm 的波长范围内,人们仅在相当有限的范围内(几微米)获得强烈的反射和光学场对结构的渗透。 超出该波长范围的光可以深入到结构中。 只是随着层对数量的增加,该“传播区域”中的强度模式仍然会变得越来越细;当然,通过这种类型的计算,人们无法得到无限光子晶体的真实能带结构。 (无论如何,现有的结构总是有限的。 然而,越来越多的层对对反射波长范围的宽度没有实质性影响;这基本上是由折射率对比度决定的(在二氧化钛和二氧化硅之间的示例案例中)。 可以证明,就相对于中心频率的光学频率而言,它是
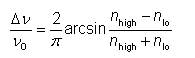
二维光子晶体
二维光子晶体结构被理解为在二维空间中是周期性的,而在第三维中没有介电常数的调制。 例如,可以考虑一个六边形结构,其中图 3 显示了一个横截面(假设 z 方向垂直于绘图平面,则对于所有z值,横截面看起来完全相同)。 气孔(以白色显示)在z方向上无限穿过结构。
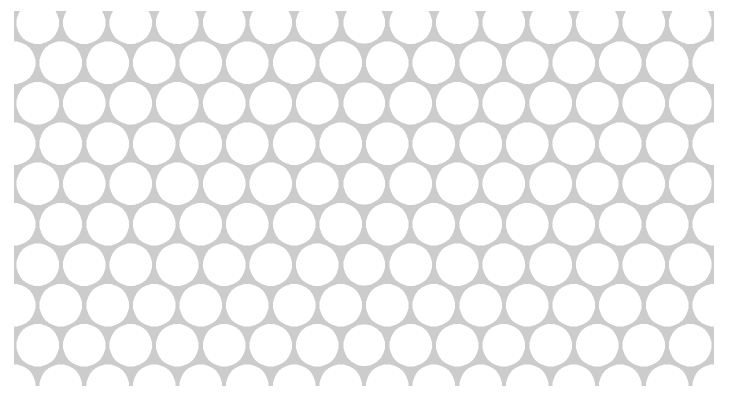
图3:横截面穿过六边形光子晶体结构,例如由玻璃(灰色)中的气孔(白色)组成。
图 3 以一个六边形结构为例,它属于特别常见的结构。 人们也可以反转这种结构,即使用被空隙包围的圆柱体图案,并通过非常细的股(光学效应可以忽略不计)或设备边缘的两个实心平面固定到位。
第三维度呢?
同样,人们可能会忽略k向量在z方向上具有分量的可能性。 这对于试图只向结构注入这种光的情况是合适的。 然而,这种情况在实际应用中很少见。 更常见的是,人们实现一个相对平坦的2D光子晶体(光子晶体板),该晶体在两侧被封闭,例如用折射率低得多的均匀材料,用经典的波导方法将光限制在该维度上。 至少光线以足够大的入射角照射到这样的界面上,可以获得全内反射。 如果光子晶体板足够薄,它可以在横向维度上具有单模特性。
另一种常见的情况是,所考虑的光或多或少地沿z方向传播。 光子晶体光纤就是这种情况 - 然而,它也需要一个额外的晶格缺陷来获得波导 - 将在下面进一步讨论。
需要强调的重要一点是,不仅计算2D光子晶体的能带结构更加困难,而且更难找到表现出完全带隙的设计,因为在一定的光学频率范围内,光根本没有方向可以传播而不会产生振幅的指数衰减。 当还考虑不同的偏振方向时,情况尤其如此。 例如,很容易发生的情况是,仅针对TE极化获得带隙,而对于TM极化则不然,反之亦然。 只有经过精心选择的结构和相对较大的折射率对比度(排除了纯标量场模型的计算),才能实现完整的带隙。 这些困难有助于人们理解,从对一维结构的最初思考到对二维光子晶体的良好理解,花了大约一个世纪的时间。
已经开发了各种技术来制造2D光子晶体结构。 与3D结构(见下文)相比,这要简单得多,主要是因为人们可以从一侧很好地进入整个结构,并且以后可能会沉积额外的均质材料,如果不是简单地使用界面空气。 有关此类技术的示例,请参阅有关光子晶体表面发射激光器的文章。 通常,人们利用在光电子学半导体加工方面已经充分开发的技术。
三维光子晶体
很容易想象各种3D光子晶体结构,例如
- 具有玻璃或半导体的球形碎片图案,排列有固态物理学中众所周知的晶格类型,例如六边形,面心立方体或金刚石结构(暂时忽略将固体碎片固定到位的必要性),
- 具有被固体介质包围的空隙倒置图案(消除了机械稳定性问题),或
- 用其它几何形状,例如获得具有不同方向的圆柱形空隙的规则图案。
3D光子晶体的制造通常更具挑战性,这一点相当明显,特别是因为短光学波长决定了微小的尺寸,以及由此产生的分辨率和精度方面的极端要求:
- 一种可能的方法是逐层构建此类结构,例如使用电子束光刻或激光3D打印技术。 然后,还可以根据需要灵活地引入晶格缺陷。 然而,这种技术在可以以这种方式加工的材料以及可以在各个方面以足够高质量的层数(例如精确的规则性、没有不规则形状等)方面受到限制。 在某些情况下,只能获得几层,总厚度只有几微米,而不是更延伸的光子晶体。
- 也可以从一块固体材料开始,然后以某种方式创建空隙图案,例如通过钻孔或反应离子蚀刻。 (这种类型的特定结构被命名为Yablonovite。 当然,这种技术仅适用于相当有限尺寸的光子晶体,因为所需的操作次数和长距离钻孔的难度随着尺寸的增加而迅速增加。
- 可以首先制造模板,例如具有紧密堆积的二氧化硅球,然后将其烧结在一起以获得机械稳定性。 然后用硅填充空隙(使用前体气体),最后通过酸蚀去除二氧化硅模板[25]。
- 有全息光刻的方法,使用干涉图案来获得大体积所需的周期性。
- 另一种可能性是使用自组装胶体晶体[52],原则上可以制成大尺寸,但很难可靠地获得所需的晶体结构。
在2D光子晶体的开创性工作之后,仅用了几年时间就找到了第一个具有完整带隙的3D光子晶体结构,并对其进行了制造。 第一个包含排列在金刚石结构中的介电球[4]。 之前关于面心立方体(fcc)结构的报告[3]必须修改。 事实证明,fcc结构通常表现出半金属带状结构(即,没有真正的带隙),尽管对于折射率对比度大于3:1的非常大的结构,完全带隙是可能的[5]。 另一种可能性是“木桩”结构,它首先在微波和中红外频率上得到证明,后来也用于近红外,包括1.5μm左右的电信波长区域[20,24]。 通过3D钨光子晶体结构,可以基本上控制热辐射的发射,使其在1.5μm左右的波长下很强,而在超过3μm的长波长下受到抑制。
全向反射;晶格缺陷
我们已经看到,光子带隙基本上禁止光在一定光学频率范围内在介质中传播。 这允许光子晶体充当一种全向反射器,假设所有相关传播方向都存在带隙 - 理想情况下,对于三维中的任何方向。 因此,光子晶体材料适用于封闭结构以防止光逸出。 事实上,Yablonovitch在1987年的开创性论文[1]已经描述了使用三维光子晶体来抑制介质内激发原子或离子的自发发射。 从量子光学中已经知道,辐射发射的可能性取决于光场的合适模式的可用性,因此光子晶体可以通过消除这种传播模式来抑制自发发射。
同样,光子晶体可用于将光限制在不同类型的结构中,这可以被认为是某种故意引入的晶格缺陷。 这些在光子带隙内提供局部缺陷状态[9]:
- 例如,如果光子晶体在固体介质中制成空隙(气孔)图案,则可以创建一个孤立的区域,其中缺少一个或几个空隙。 结果可以是一个微小的光学谐振器,称为微谐振器或微腔[13]。 如果只使用直径减小的气孔而不是完全缺失的孔,或者仅修改尺寸或定位的其他特征,则这种谐振器的Q因数特别高是可能的[40]。 关于制造公差的优化也很重要[43],因为制造技术的缺陷不能随意减少。 高Q因子与光放大元件(通常是量子点)相结合,也允许形成具有低阈值泵浦功率的微激光器[31]。 虽然其他类型的微谐振器(例如环形微腔)可能达到更高的Q因数,但光子晶体微腔具有关键优势,即更容易与采用相同技术制成的波导进行良好控制的耦合。
- 这种去除的空隙的一长串可以充当通道波导。 类似地,通过二维扩展晶格缺陷可以得到一种平面波导。 通道波导通常只能在一定方向上运行,不能在横向上任意移动,因为有与光子晶体结构一致的要求。 然而,甚至可以实现突然转向其他方向(例如直角转弯)[11],这对于传统波导会导致巨大的功率损耗。 此外,可以实现各种类型的波导结(例如T结)和分束器[29],例如用于干涉仪。 附近的波导可以在短时间内表现出非常强的耦合。
- 如果两个或多个这样的结构之间有足够小的距离,它们之间可能存在一些耦合。 例如,谐振器可以耦合到波导,这样就可以通过波导注入光,然后波导将在某个狭窄的频率范围内有效地进入谐振器,并且可能耦合到也耦合到谐振器的第二个波导。 通过这种方式,可以构建高度频率敏感的耦合器。

图4:具有晶格缺陷的2D光子晶体结构,形成两个波导和一个耦合到它们的谐振器。该图仅作为说明,并不声称它正是经过充分分析和优化的结构。
有意引入某些晶格缺陷的概念,例如谐振器和波导,以及集成的发光特征,也适用于三维。 只是,实施起来还是相当困难的,并且要优化设计这样的结构。 需要考虑由缺陷引起的波导传播损耗[33]。 尽管如此,还是有一些结果:
- 已经证明,发光量子阱可以集成到3D“木桩”光子晶体结构中,并且已经证明了光子晶体对发光的抑制和作为光学谐振器的点缺陷对发射特性的改变[42]。
- 反蛋白石光子晶体结构中的半导体量子点也实现了类似的事情[44]。
各种特殊效果
除了抑制光在某些频率区域的传播之外,光子晶体还可以提供广泛的特殊效果:
- 已经提到,光子晶体(带隙区域之外)中的光群速度可能非常不寻常,例如远低于正常(慢光)。
- 在某些情况下,会发生负折射[41,36] - 正如具有负折射率的材料所预期的那样:在与光子晶体材料的界面之后,反射光束与入射光束发生在法线方向的同一侧。
- 另一种可能性是超折射,其中介质的行为类似于折射率低于单位的介质。
- 在某些情况下,光在光子晶体上的折射表现出输出传播方向对输入方向或光波长的异常强依赖性;这种超棱镜效应[16,18,19]已经在理论和实验上进行了研究。
- 使用光子晶体材料板[38]进行亚波长成像(超透镜)是可行的,该材料还可以捕获倏逝波以实现超分辨率。
- 自准直意味着注入的光束(频率在光子波段内)在没有明显光束发散的情况下传播 - 并且不使用任何波导结构。 因此,它无需对波导输入进行任何关键对准,也适用于具有一定传播方向范围的波束。
计算方法
对光子晶体材料和相关器件的能带结构进行详细分析不仅对于获得对这些结构和器件的良好定量理解至关重要,而且对于成功的设计优化也至关重要。 它需要相当复杂的数学和计算工具 - 特别是如果需要全面的3D模型。 正如已经指出的那样,由于必要的大折射率对比度,通常需要对电磁场进行完整的矢量描述。 已经开发了相当不同的技术,这些技术可能具有特定的优势(例如准确性和计算效率),但也存在严重的局限性,例如仅适用于特定情况:
- 有限差分时域(FDTD)仿真[17]允许人们灵活地模拟时变现象,例如超短脉冲在光子晶体波导中的传播,经历色散和非线性的影响。 这些方法非常通用,但往往会导致大量的计算负载并需要大量的计算机内存 - 特别是如果调查具有相对较大的容量的设备。
- 光束传播方法可以大大提高效率,但在应用中受到更多限制。 它们通常仅适用于特殊结构,也适用于单色场,并且通常不能用于模拟随时间变化的过程,尤其是在涉及非线性效应时。
- 平面波方法[4]在空间频域中工作。 在这里,光场被分解成有限(但大量)具有不同传播方向的平面波,这些平面波通过光子晶体结构相互耦合。 不同平面波的复系数可以用矩阵法计算[7,12]。
- 这种技术更有效(但更难实现)的变体用一组不同的功能取代了平面波,这些功能更好地反映了传播模式的属性。 例如,可以使用 Wannier 函数或多极展开。 然后需要较少数量的此类函数和相应的较小矩阵。
- 对于3D光子晶体,有转移矩阵方法,其中光子晶体被认为是不同衍射光栅的堆栈。 对于这种堆栈的每一层(通常只有几种类型),可以计算耦合矩阵,例如使用有限元方法。 通过将获得的矩阵相乘,可以得到代表整个光子晶体的矩阵。
一个特别困难的领域是全面研究具有晶格缺陷和随机缺陷的3D光子晶体结构的影响,这可能是由于制造方法的缺陷造成的。 即使在现代计算机上,这种计算在计算时间和所需的计算机内存方面也相当苛刻。
由于这种计算方法的至关重要性及其难度,科学研究和实际应用的进展在很大程度上取决于该领域的进展。
光子晶体结构的应用
在前面的段落中,重点是物理基础,但已经提到了一些可能的应用。 事实上,至少可以想象广泛的应用,尽管只有一小部分已被证明适合广泛的实际使用。 下面简要总结了可能的应用。
量子光学研究
光子晶体引起的电磁模式结构的实质性变化对自发发射具有深远的影响。 这在量子光学中可以解释,并且是光子晶体在各种量子光学实验中使用的基础进行基础研究。 但是,也有各种实际用途,如以下各节所述。
单模发光二极管
单模LED有点类似于微型激光器 - 但它没有激光谐振器。
发光二极管通常发射到非常多的辐射模式,即基本上没有空间相干性。 然而,这可以通过用光子晶体强烈修改辐射场的模态结构来改变。 在极端情况下,人们会获得单模LED,它将大部分输出功率发射到单模中。 这允许有效地耦合到单模波导中。 此类器件还允许非常高的调制频率[51],这对于通信应用非常重要。 例如,这种单模LED可能会与VCSEL竞争。
光子集成电路
对于光纤通信、光学计量等领域的应用,获得强大的光子集成电路的前景多年来一直是研究的重要推动力,尽管事实证明以合理的成本制造出工作良好的设备是相当困难的。
通常,利用光子带隙将光限制在谐振器或波导上,谐振器或波导可以相互耦合。 大量的工作集中在2D光子晶体上,主要是因为它们比3D结构更容易制造,并且足以满足许多目的。 然而,3D光子芯片将为在相当小的体积中实现复杂功能提供显着增加的潜力。
除了谐振器中波导的形成之外,还可以利用一系列物理效应。 一些例子:
- 精确的滤光片可以通过包含高Q谐振器的结构与波导耦合,使用各种干涉仪来实现,并且可能基于超棱镜效应[35]。 典型的应用是用于光纤通信中波分复用的分复用的分接复用器。
- 由于循环光功率的强烈共振增强,高Q谐振器可以表现出实质性的非线性效应[46,48]。 例如,人们可以利用它进行信号处理或生成额外的波长分量。
- 具有非常低泵浦阈值的激光器(基本上是无阈值激光器)也可以实现并方便地在芯片上用作相干光源。
光子晶体光纤
光子晶体光纤[37]是二维光子晶体结构的一个例子,其中光传播主要在大约垂直于光子晶体平面的方向上。 通常,人们有一些规则图案的气孔,其亚微米直径贯穿光纤的整个长度。 常见的设计在中心有一个缺失的孔,形成光纤波导。 然而,还有许多更复杂的设计 - 例如,空心光纤,部分依赖于光子带隙。
请注意,并非所有微结构光纤都是真正的光子晶体光纤,因为它们中的一些缺乏实际的晶体对称性。
有关更多详细信息,请参阅有关光子晶体光纤的文章。
光子晶体表面发射激光器
有一种半导体激光器,称为光子晶体表面发射激光器,其增益区域是二维光子晶体结构[22,28]。 这有助于确保尽管发射面积很大,但具有高空间相干性的发射。 因此,结合高输出功率水平,可以实现非常高的光束质量。
有关更多详细信息,请参阅有关光子晶体表面发射激光器的文章。
热排放控制
热发射在白炽灯中发光的应用已经很长时间了。 一个根本问题一直是,发射的光谱形状只能通过工作温度在相当有限的程度上控制;发射功率的最大部分位于不可用的红外光谱区域。 虽然可以通过提高工作温度来提高可见光的产生效率,但会遇到设备寿命有限的问题。 如果可以通过使用光子带隙效应来抑制长波长发射,情况可能会大大改善。 尽管到目前为止,在这个方向上只取得了有限的技术进步,但至少可以想象,在未来,灯泡的能源效率将大大提高,理论上甚至可以与发光二极管(LED)竞争。
对热发射的类似控制也可能非常有用,即使它只在近红外中起作用。 然后可以使用这种发射在光伏电池中发电。 从理论上讲,基于已经证明的发射结构,效率甚至可能超过30%[34]。 因此,例如,有可能以合理的效率将废热转化为电能。
参考文献
[1] E. Yablonovitch, “Inhibited spontaneous emission in solid-state physics and electronics”, Phys. Rev. Lett. 58 (20), 2059 (1987), doi:10.1103/PhysRevLett.58.2059
[2] S. John, “Strong localization of photons in certain disordered dielectric superlattices”, Phys. Rev. Lett. 58 (23), 2486 (1987) doi:10.1103/PhysRevLett.58.2486
[3] E. Yablonovitch and T. J. Gmitter, “Photonic band structure: the face-centered cubic case”, Phys. Rev. Lett. 63 (18), 1950 (1989), doi:10.1103/PhysRevLett.63.1950
[4] K. M. Ho, C. T. Chan and C. M. Soukoulis, “Existence of a photonic gap in periodic dielectric structures”, Phys. Rev. Lett. 65 (25), 3152 (1990), doi:10.1103/PhysRevLett.65.3152
[5] E. Yablonovitch and T. J. Gmitter, “Photonic band structure: the face-centered cubic case”, J. Opt. Soc. Am. A 7 (9), 1792 (1990), doi:10.1364/JOSAA.7.001792
[6] E. Yablonovitch, T. J. Gmitter and K. M. Leung, “Photonic band structure: the phase-centered-cubic case employing nonspherical atoms”, Phys. Rev. Lett. 67 (17), 2295 (1991), doi:10.1103/PhysRevLett.67.2295
[7] J. B. Pendry and A. MacKinnon, “Calculation of photon dispersion relations”, Phys. Rev. Lett. 69 (19), 2772 (1992), doi:10.1103/PhysRevLett.69.2772
[8] E. Yablonovitch, “Photonic band-gap structures”, J. Opt. Soc. Am. B 10 (2), 283 (1993), doi:10.1364/JOSAB.10.000283
[9] R. D. Meade et al., “Novel applications of photonic bandgap materials: Low-loss bands and high Q cavities”, J. Appl. Phys. 75, 4753 (1994), doi:10.1063/1.355934
[10] P. R. Villeneuve and M. Piché, “Photonic bandgaps in periodic dielectric structures”, Progress in Quantum Electronics 18 (2), 153 (1994), doi:10.1016/0079-6727(94)90007-8
[11] A. Mekis et al., “High transmission through sharp bends in photonic crystal waveguides”, Phys. Rev. Lett. 77 (18), 3787 (1996), doi:10.1103/PhysRevLett.77.3787
[12] J. B. Pendry, “Calculating photonic band structure”, J. Phys: Condensed Matter 8 (9), 1085 (1996)
[13] J. Foresi et al., “Photonic-bandgap microcavities in optical waveguides”, Nature 390 (6656), 143 (1997), doi:10.1038/36514
[14] S. Y. Lin et al., “A three-dimensional photonic crystal operating at infrared wavelengths”, Nature 394, 251 (1998), doi:10.1038/28343
[15] , S. Fan et al., “Channel drop tunneling through localized states”, Phys. Rev. Lett. 80 (5), 960 (1998), doi:10.1103/PhysRevLett.80.960
[16] H. Kosaka et al., “Superprism phenomena in photonic crystals”, Phys. Rev. B 58, R10096 (1998), doi:10.1103/PhysRevB.58.R10096
[17] J. Arriaga, A. J. Ward and J. B. Pendry, “Order-N photonic band structures for metals and other dispersive materials”, Phys. Rev. B 59 (3), 1874 (1999), doi:10.1103/PhysRevB.59.1874
[18] H. Kosaka et al., “Superprism phenomena in photonic crystals: toward microscale lightwave circuits”, J. Lightwave Technol. 17 (11), 2032 (1999), doi:10.1109/50.802991
[19] H. Kosaka et al., “Photonic crystals for micro lightwave circuits using wavelength-dependent angular beam steering”, Appl. Phys. Lett. 74, 1370 (1999), doi:10.1063/1.123553
[20] J. G. Fleming and S. Y. Lin, “Three-dimensional photonic crystal with a stop band from 1.35 to 1.95 μm”, Opt. Lett. 24 (1), 49 (1999), doi:10.1364/OL.24.000049
[21] H. B. Sun, S. Matsuo and H. Misawa, “Three-dimensional photonic crystal structures achieved with two-photon-absorption photopolymerization of resin”, Appl. Phys. Lett. 74, 786 (1999), doi:10.1063/1.123367
[22] M. Imada et al., “Coherent two-dimensional lasing action in surface-emitting laser with triangular-lattice photonic crystal structure”, Appl. Phys. Lett. 75 (3), 316 (1999), doi:10.1063/1.124361
[23] B. Gralak, S. Enoch and G. Tayeb, “Anomalous refractive properties of photonic crystals”, J. Opt. Soc. Am. A 17 (6), 1012-1020 (2000), doi:10.1364/JOSAA.17.001012
[24] S. Noda et al., “Full three-dimensional photonic bandgap crystals at near-infrared wavelengths”, Science 289 (5479), 604 (2000), doi:10.1126/science.289.5479.604
[25] A. Blanco et al., “Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres”, Nature 405, 437 (2000), doi:10.1038/35013024
[26] J. E. Sipe, “Vector k·p approach for photonic band structures”, Phys. Rev. E 62 (4), 5672 (2000), doi:10.1103/PhysRevE.62.5672
[27] S. G. Johnson et al., “Multipole-cancellation mechanism for high-Q cavities in the absence of a complete photonic band gap”, Appl. Phys. Lett. 78 (22), 3388 (2001), doi:10.1063/1.1375838
[28] S. Noda et al., “Polarization mode control of two-dimensional photonic crystal laser by a unit cell structure design”, Science 293 (5532), 1123 (2001), doi:10.1126/science.1061738
[29] S. Fan et al., “Waveguide branches in photonic crystals”, J. Opt. Soc. Am. B 18 (2), 162 (2001), doi:10.1364/JOSAB.18.000162
[30] Y. A. Vlasov et al., “On-chip natural assembly of silicon photonic bandgap crystals”, Nature 414, 289 (2001), doi:10.1038/35104529
[31] M. Lončar, T. Yoshie and A. Scherer, “Low-threshold photonic crystal laser”, Appl. Phys. Lett. 81, 2680 (2002), doi:10.1063/1.1511538
[32] B. Temelkuran et al., “Wavelength-scalable hollow optical fibres with large photonic bandgaps for CO2 laser transmission”, Nature 420, 650 (2002), doi:10.1038/nature01275
[33] C. Sell et al., “Propagation and loss in three-dimensional photonic crystal waveguides with imperfect confinement”, Phys. Rev. B. 68, 113106 (2003), doi:10.1103/PhysRevB.68.113106
[34] S. Y. Lin, J. Moreno and J. G. Fleming, “Three-dimensional photonic-crystal emitter for thermal photovoltaic power generation”, Appl. Phys. Lett. 83, 380 (2003), doi:10.1063/1.1592614
[35] T. Prasad, V. Colvin and D. Mittleman, “Superprism phenomenon in three-dimensional macroporous polymer photonic crystals”, Phys. Rev. B 67, 165103 (2003), doi:10.1103/PhysRevB.67.165103
[36] E. Cubukcu et al., “Negative refraction by photonic crystals”, Nature 423, 604 (2003), doi:10.1038/423604b
[37] P. St. J. Russell, “Photonic crystal fibers” (review paper), Science 299, 358 (2003), doi:10.1126/science.1079280
[38] C. Luo et al., “Subwavelength imaging in photonic crystals”, Phys. Rev. B 68 (4), 045115 (2003), doi:10.1103/PhysRevB.68.045115
[39] K. Srinivasan et al., “Experimental demonstration of a high quality factor photonic crystal microcavity”, Appl. Phys. Lett. 83 (10), 1915 (2003), doi:10.1063/1.1606866
[40] K. Srinivasan and O. Painter, “Fourier space design of high-Q cavities in standard and compressed hexagonal lattice photonic crystals”, Opt. Express 11 (6), 579 (2003), doi:10.1364/OE.11.000579
[41] S. Foteinopoulou, E. N. Economou and C. M. Soukoulis, “Refraction in media with a negative refractive index”, Phys. Rev. Lett. 90, 107402 (2003), doi:10.1103/PhysRevLett.90.107402
[42] S. Ogawa et al., “Control of light emission by 3D photonic crystals”, Science 305 (5681), 227 (2004), doi:10.1126/science.1097968
[43] K. Srinivasan, P. E. Barclay and O. Painter, “Fabrication-tolerant high quality factor photonic crystal microcavities”, Opt. Express 12 (7), 1458 (2004), doi:10.1364/OPEX.12.001458
[44] P. Lodahl et al., “Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals”, Nature 430, 654-657 (2004), doi:10.1038/nature02772
[45] A. Rodriguez et al., “Disorder-immune confinement of light in photonic-crystal cavities”, Opt. Lett. 30 (23), 3192 (2005), doi:10.1364/OL.30.003192
[46] M. Notomi et al., “Optical bistable switching action of Si high-Q photonic-crystal nanocavities”, Opt. Express 13 (7), 2678 (2005), doi:10.1364/OPEX.13.002678
[47] M. Fujita et al., “Simultaneous inhibition and redistribution of spontaneous light emission in photonic crystals”, Science 308 (5726), 1296-1298 (2005), doi:10.1126/science.1110417
[48] J. Bravo-Abad et al., “Enhanced nonlinear optics in photonic-crystal microcavities”, Opt. Express 15 (24), 16161 (2007), doi:10.1364/OE.15.016161
[49] S. Noda, M. Jujita and T. Asano, “Spontaneous-emission control by photonic crystals and nanocavities”, Nature Photonics 1 (8), 449 (2007), doi:10.1038/nphoton.2007.141
[50] R. H. Lipson and C. Lu, “Photonic crystals: a unique partnership between light and matter”, Eur. J. Phys. 30, S33 (2009), doi:10.1088/0143-0807/30/4/S04
[51] G. Shambat et al., “Ultrafast direct modulation of a single-mode photonic crystal nanocavity light-emitting diode”, Nature Communications 2, 539 (2011), doi:10.1038/ncomms1543
[52] Z. Cai et al., “From colloidal particles to photonic crystals: advances in self-assembly and their emerging applications”, Chemical Society Reviews 10 (50), 5898 (2021), doi:10.1039/D0CS00706D



