定义
单位面积和立体角的光功率。
辐射度是一个辐射量。它可以为光源和到达某个位置的光定义,如以下两节所述。从本质上讲,辐射度可以被认为是每单位面积的辐射强度,但真正了解该主题需要更多的思考,如下所述。
到达光的辐射率
到达光的辐射度定义如下:我们考虑一种情况,即来自扩展光源的光照射到某个小区域,该区域(首先考虑)的方向使其以垂直方式被光线照射。辐照度E是撞击该区域的光功率除以该区域的大小。辐射度L是每立体角的辐照度,或单位面积和立体角的光功率。该立体角是指上述区域从光源接收光线的方向。该立体角的顶点位于所考虑区域的中心。(请务必始终使用与所考虑区域相对应的顶点;区域元素和方向圆锥是在一起的。
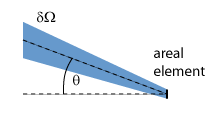
图1:来自某个方向(在某个立体角内δΩ)的入射光会在面元素上产生一些辐射。
我们可以将其推广到非正常发病率(见图1);然后,我们还需要除以cos θ(θ是入射角,相对于法线方向测量),以便考虑到我们可以通过将面元素定向到源来获得更多的功率。
辐射度通常是位置和观察方向的函数。如果光源在其区域内均匀辐射,则辐射度将独立于跨越光源大小的特定观察方向范围内的观察方向。
到达我们的面元件的总光功率可以被认为是由来自不同入射方向的元件不同部分的贡献组成:
辐射的基本单位是W m−2 sr−1 (瓦特/平方米和球面度),或更常见的是W cm−2 sr−1 。
辐射也可以进行光谱分辨,即分解为不同波长或光学频率的贡献;总辐射度可以写为
哪里Lλ是相对于波长的光谱辐射度;光学频率也可以做到这一点。的单位Lλ是 W cm−2 sr−1 nm−1 ,以及那些Lν是 W cm−2 sr−1 Hz−1。
示例:太阳光的辐射和相关眼睛危害
作为一个例子,我们考虑照射人眼的阳光,人眼朝向太阳。接收到的辐射度是辐照度(例如 520 W/m2)除以立体角,立体角与地球上太阳的角度副时态有关。后者约为 α = 10 mrad,导致立体角Ω = π α2/ 4= 79 ·10−6sr 。由此产生的辐射度为6.6 · 106 W m−2 sr−1 = 660 W cm−2 sr−1 在这种潜态中近似恒定,当我们忽略太阳耀斑等细节时。
太阳的光辉与距离无关!
有趣的是,太阳光的辐射度与距离无关(除了在某种意义上非常大的距离,见下文)。这是因为在较远的距离(例如在火星上),辐照度较低,但角度副张力也较低:在那里,太阳看起来更小,但并不那么亮。
通过望远镜观察太阳是危险的,但光芒不会增加!
此外,当通过望远镜观察太阳时,太阳光(或来自月球的光)的辐射也不会增加;一般来说,镜片不能增加光泽。虽然眼睛瞳孔处相关性较低的辐射可以通过望远镜显着增加,但视网膜图像也会增加,因此视网膜辐照度无法增加。然而,通过望远镜观察太阳是危险的,因为它增加了进入眼睛和视网膜上照明区域的总光功率,因此由于径向热流减少,视网膜的加热变得更强。即使没有望远镜,也不建议直接观察太阳。
由于辐射的恒定性(只要在到达观察者的途中没有光损失),人们实际上可以认为辐照度是太阳的一个属性,而不是最初定义的场量。
虽然眼睛入口处的辐照度与眼睛瞳孔面积一起决定了到达眼睛视网膜的总光功率(忽略了眼睛中的一些功率损失),但辐射度决定了视网膜上产生的光学强度(或辐照度),因为视网膜图像的角度亚张力与从眼睛外看到的太阳的角度亚张力相同。(为了理解后一种说法,请考虑来自太阳不同部分的光线穿过眼睛晶状体的中心 - 它们不会在那里偏转。
视网膜的辐照度当然是一个重要因素(除了一些其他细节,如照射区域和光谱质量)辐射对眼睛有多危险。因此,辐射度而不仅仅是入射辐射的辐照度(在眼睛外看到)是与安全性更相关的因素。在眼睛内部,视网膜的辐照度很重要,但辐射度是眼睛外的一个量,与眼睛的特定特性无关,可用于量化眼睛危害。
但是请注意,视网膜的风险还取决于照射区域的大小,因为由此产生的温度升高取决于此。
遥远恒星的辐射率
上述考虑表明,恒星的辐射度原则上与观测距离无关。然而,感知距离显然取决于该距离。这与遥远恒星的角度副时态远远小于眼睛的分辨率极限有关。为了考虑到这一点,人们可以根据1.5 mrad的角度次级(人眼通常使用的值)而不是恒星实际上小得多的次级来计算有效辐射度。然后,结果与观测距离的平方成反比,与感知亮度的变化一致。
这个例子表明,感知的亮度并不严格地取决于物理辐射,因为眼睛的角度分辨率有限。
例如,从地球或更远的距离观察月球时,情况就大不相同了。在这里,眼睛可以很容易地分辨一个圆盘,视亮度不依赖于观察距离。
激光安全背景下激光束的辐射
在激光安全的背景下,辐照度不是简单地基于本文开头给出的物理定义计算的,而是经过一些修改:
- 只要激光束的直径小于眼睛瞳孔的直径,从而不会发生截断,眼睛的辐照度是通过将光功率除以瞳孔面积来计算的——这导致平均辐照度,其可以大大低于光束轴上的辐照度。
- 假设光束发散度低于 1.5 mrad(全角度),根据眼睛的限制,假设全角度为 1.5 mrad。
因此,很明显,物理定义的辐射不能直接用于评估激光危害;一个需要考虑到人眼基本特性的修改。
以角分辨率测量辐射度
来自光源的光的辐射度可以通过成像设置进行技术测量,如图2所示。

图2:测量辐射度的仪器。在本例中,光学器件聚焦到无穷远,以测量远处物体的辐射度。
在最简单的情况下,使用的光电探测器是光电二极管,例如,没有任何空间分辨率。它充当视场挡块,即其尺寸与到透镜的距离决定了可以检测辐射的视野。区域元素由光圈光圈定义。为了获得辐射度,探测器记录的光功率除以孔径光阑的面积和根据视场的立体角。获得的辐射度是孔径区域和视场的平均值。对于高角度分辨率,需要使用小型探测器,从而产生小视野。
光电探测器当然可以用图像传感器代替,这样就可以在视场内对结果进行空间分辨。然后基本上有一个相机,可以校准绝对辐射测量。每个像素都与一个小的查看方向子范围相关联。入射到物镜上的光没有达到空间分辨率,但光学入口上的辐照度通常是相当均匀的。可能还必须考虑光谱域;例如,可以使用光学带通滤光片来测量某个小波长间隔内的光谱辐射度。
光源的辐射度
辐射的概念也可以应用于光源。在这里,人们取光源本身的光学强度 - 例如,在发射光的光学孔径处 - 以及发射光的角度分布。由此产生的辐射度(通常是位置和角方向的函数)表示放置在某个方向上的探测器将看到多少光。但是,这不是使用该概念的唯一方法,如下所示。
光源辐射度与探测器辐射度的关系
我们现在考虑光源的辐射度与通过自由空间传播后到达某个可检测表面的辐射之间的关系。
我们假设有一个面积均匀的发光源一个s,具有光泽Ls在围绕法线方向的某些角度范围内,它与方向近似无关。此外,我们假设在距离光源一定距离d处,我们有一个探测器表面一个d(例如,光电二极管的有效面积)。从光源看,探测器表面的立体角Ad / d2 。因此,到达探测器表面的光功率为Pd = Ls As Ad / d2。
从探测器看到的光源的立体角As / d2 。因此,探测器处的辐射度为 Ld = Pd / (Ad As / d2) 。我们发现探测器的辐射确实与源辐射相同Ls。因此,人们实际上可以选择从光源的角度或探测器或其他位置的角度计算辐射度。只是,必须始终使用与所考虑的面元素的顶点相对应的立体角。
当然,在其他情况下,辐射的保存通常不会成立,例如在光源和探测器之间吸收或散射物体。
激光源的辐射度
激光源的亮度通常根据辐射的概念进行评估,但形式有所修改 - 完全超出了激光安全的范围。目标是获得在限制条件下聚焦激光的强度的度量(例如,使用有限尺寸的透镜聚焦给定距离)。
在这里,人们考虑通过光束焦点的平面(例如,如果原始激光束准直,则可能与透镜形成)。为简单起见,我们首先假设具有一定光束半径的高斯光束 w0在焦点和半角发散θ中,并且我们有足够小的角度,使得可以使用近轴近似。然后我们可以将光强度定为I = P / π w2,其实是一种平均值;同轴强度实际上高出两倍。同样,我们可以使用立体角Ω = π θ2.通过将其正式插入辐射的定义中,我们得到:

请注意,这种辐射是表征激光束或其光源的单一值,不再是场量(取决于位置和方向)。也可以将其视为最佳方向的辐射,即沿光束的辐射。
例如,假设衍射限制光束质量,我们可以在 635 nm 处使用具有 1 mW 的激光指示器;那么辐射度是 2.5 ·105W cm−2 sr−1。该值比上面计算的太阳高几个数量级。然而,眼睛的危害与太阳大致相当,因为潜在的非常小的光束发散与眼睛无关。
对于具有非理想光束质量的激光器,辐射率的结果可以推广,量化为M2因素在两个方向上:
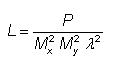
这表明辐射度(亮度)基本上取决于功率和光束质量,而不是波长。
下表包含不同类型激光器的辐射值的一些示例:
| 激光 | 辐射率 |
|---|---|
| 激光指示器,635 nm 处为 1 mW,衍射极限 | 248 kW cm−2 sr−1 |
| 广域半导体激光管,808 nm 时为 5 W,M2= 20 / 1.5 | 26 MW cm−2 sr−1 |
| 光纤耦合半导体激光管棒, 808 nm 时为 100 W, 600 μm 光纤, NA 0.22 | 234 kW cm−2 sr−1 |
| 光纤耦合半导体激光管堆栈,808 nm 时为 400 W,600 μm 光纤,NA 0.22 | 935 kW cm−2 sr−1 |
| Nd:YAG 激光器,1064 nm 处为 1 W,衍射极限 | 88 MW cm−2 sr−1 |
| Yb:YAG 薄盘激光器,1 kW 在 1030 nm 处,M2= 8 | 1.47 GW cm−2 sr−1 |
| Yb:YAG 薄盘激光器,1030 nm 处为 1 kW,衍射极限 | 94 GW cm−2 sr−1 |
| CO2激光, 10.6 μm 时为 1 kW,衍射极限 | 0.9 GW cm−2 sr−1 |
表 1:不同激光源的辐射值。
这表明具有较高输出功率的激光器不一定表现出更高的辐射度。请注意,仅考虑了连续波激光器;脉冲激光器可以具有非常高的峰值功率,因此在脉冲期间具有更高的辐射度。
具有高辐射度的激光或其他光源应称为高辐射源,它比高亮度光源更准确。
此处定义的辐射度决定了焦点的最大光学强度,该焦点可以在一定的孔径尺寸和工作距离下产生,即具有有限的光束发散。如果我们假设我们可以生成一个光束焦点,其中发散半角 θ 受上述参数的限制,则立体角为π θ2。通过将激光的辐射度乘以该辐射,我们获得了焦点的强度。这至少是一个粗略的估计,没有考虑到强度分布的详细空间形状。
因此,辐射度可以被视为一个明确定义的量,即激光亮度的一种定量度量,与高光学强度的产生具有直接的实际相关性。
泵浦和激光的辐射度
请注意,光泵浦激光器的辐射度通常远高于其泵浦源的辐射度。被动光学系统无法实现如此增加的辐射,但是利用受激发射效应的激光设备确实可以充当所谓的亮度转换器。
在光学泵浦激光器的开发中,使用低辐射的泵浦源通常有明显的动机:对于给定的输出功率水平,这种源通常更便宜。例如,广域激光二极管(也称为高亮度半导体激光管)的每瓦输出功率价格高于二极管条,而弧光灯或闪光灯的每瓦成本最低,其辐射度非常低。然而,较低的泵浦辐射会对激光设计产生各种不利影响。由于各种原因(在不同情况下可能有很大差异),在这种情况下,在输出功率、功率效率、脉冲持续时间或脉冲重复率方面可实现的激光性能通常较低。
这种限制让人想起能量转换过程中的熵问题:熵增加过程可能不会导致能量的直接损失,但通常会导致可用能量(exergy)的间接损失。请注意,由于光束质量损失而导致的辐射(亮度)劣化基本上意味着辐射从少数模式传播到多种模式,这确实增加了熵。然而,上述性能损失并不总是与熵问题直接相关,而是部分与限制有关,例如可用增益介质的物理参数,有时与几何问题有关。
光源和散射体具有与方向无关的辐射
虽然激光通常表现出非常强烈地依赖于观察方向的辐射,但有些光源发出的光与方向无关。为了在观测方向上完全独立,人们将有一个朗伯光源。关于该主题的文章还解释了与方向无关的辐射如何与朗伯余弦定律一致,指出辐射强度与观察角度的余弦成正比。
朗伯特征更常在光散射的背景下遇到。有相对接近朗伯特征的光学扩散器。
参考文献
[1] K. Schulmeister, “The radiance of the sun, a 1 mW laser pointer and a phosphor emitter”, ILSC 2013 conference proceedings, available on the author's website



