定义
仅具有量子噪声的单频激光器的线宽。
甚至在第一个激光器被实验证明之前,肖洛和汤斯就计算了激光器线宽的基本(量子)极限[1]。这导致了肖洛-汤斯方程,它成为激光物理学最着名的方程之一:
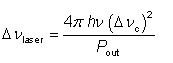
用光子能量hν,谐振器带宽 Δνc(半宽在半最大值,HWHM)和输出功率 P外。据推测,没有寄生腔损失。请注意,结果被解释为半角最大值处的半宽。
后来,梅尔文·拉克斯(Melvin Lax)表明,激光操作中的线宽(高于阈值泵功率)必须比肖洛和汤斯[2]得出的线宽小两倍。如果我们考虑因子1 / 2,并将线宽值转换为半最大值(FWHM)的全宽(对于激光线宽和腔体线宽),这是更常见的,我们得到修改后的线宽方程
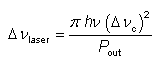
等式[6,8]的更一般形式是
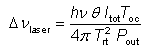
哪里T噢噢表示输出耦合器传输,l托特总谐振器损耗(可能大于T噢噢),T断续器谐振器往返时间和θ自发发射因子,其中考虑了(准)三电平增益介质中自发发射的增加。
相位噪声的相应双侧功率谱密度为
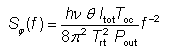
这对应于白噪声
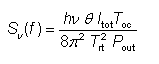
从本质上讲,Schawlow-Townes线宽是由量子噪声引起的光学相位波动强度决定的。
人们通常声称,对应于Schawlow-Townes线宽的相位噪声水平是自发发射到激光模式的结果。虽然这张图片很直观,但并不完全正确。激光增益和激光谐振器的线性损耗都会向腔内光场贡献等量的量子噪声。这意味着,即使用一些无噪声放大过程代替激光增益,相位噪声也只会降低到Schawlow-Townes值的一半[3]。
精心构造的固态激光器在几千赫兹的范围内可以具有非常小的线宽,这仍然远远高于其Schawlow-Townes极限:技术上过量的噪声使得很难达到该极限。
半导体激光器的线宽通常也比原始方程(不带α因子)大得多:
- 还有一个自发发射因子,例如2或3的数量级,由于半导体中的重吸收。
- 更重要的是,存在较强的幅相耦合效应,可以用线宽增强因子α量化,并且可以使线宽增加一个因子1 + α2,这可以贡献超过一个数量级。
- 此外,可以存在具有1/f型形状的瞬时频率的功率谱密度的过量噪声。这与半导体中电荷载流子的波动有关。
- 特别是对于外腔二极管激光器,由于机械振动,也可能存在明显的过量噪声。
锁模激光器的应用
有趣的是,Schawlow-Townes公式甚至可以应用于主动锁模激光器[4],使用总平均功率(而不是频率梳特定行的功率)用于P外.后一条规则可能令人惊讶,但考虑到光谱中各条线的相位不能独立演化,可以理解;它们被调制器锁定在一起。(否则,循环脉冲将崩溃。
对于被动锁模激光器,可以进一步推广[5]。在这里,肖洛-汤斯公式提供了靠近光谱中心的线宽的估计值,而光谱机翼中的线宽由于量子噪声引起的时序抖动而有所增加。然而请注意,许多被动锁模激光器中发生的非线性动力学可能导致强烈的过量噪声,从而使此类情况下的肖洛-汤斯结果无效。
参考文献
[1] A. L. Schawlow and C. H. Townes, “Infrared and optical masers”, Phys. Rev. 112 (6), 1940 (1958), doi:10.1103/PhysRev.112.1940 (contains the famous Schawlow–Townes equation)
[2] M. Lax, “Classical noise. V. Noise in self-sustained oscillators”, Phys. Rev. 160 (2), 290 (1967), doi:10.1103/PhysRev.160.290
[3] H. M. Wiseman, “Light amplification without stimulated emission: beyond the standard quantum limit to the laser linewidth”, Phys. Rev. A 60 (5), 4083 (1999), doi:10.1103/PhysRevA.60.4083
[4] P.-T. Ho, “Phase and amplitude fluctuations in a mode-locked laser”, IEEE J. Quantum Electron. 21 (11), 1806 (1985), doi:10.1109/JQE.1985.1072594
[5] R. Paschotta et al., “Optical phase noise and carrier–envelope offset noise of mode-locked lasers”, Appl. Phys. B 82 (2), 265 (2006), doi:10.1007/s00340-005-2041-9
[6] R. Paschotta, "Derivation of the Schawlow–Townes linewidth"
[7] C. J. McKinstrie, T. J. Stirling and A. S. Helmy, “Laser linewidths: tutorial”, J. Opt. Soc. Am. B 38 (12), 3837 (2021), doi:10.1364/JOSAB.439882
[8] R. Paschotta, H. R. Telle, and U. Keller, “Noise of Solid State Lasers”, in Solid-State Lasers and Applications (ed. A. Sennaroglu), CRC Press, Boca Raton, FL (2007), Chapter 12, pp. 473–510



