定义
非线性和色散介质中的光脉冲,其时间和光谱形状发生周期性振荡。
一种基本的孤子为传播在色散介质(例如,光纤)中,具有固定的时间强度曲线(即色散不会引起任何时间展宽)的光脉冲。当脉冲具有固定形状并且能量由介质中的参数(尤其是色散和非线性)和脉冲长度决定。
高阶孤子是能量为基本孤子整数的平方倍(即,4,9,16等)的孤子脉冲。该脉冲的时间兴中并不是常数,而是在传播过程中周期性变化(见图1和图2)。
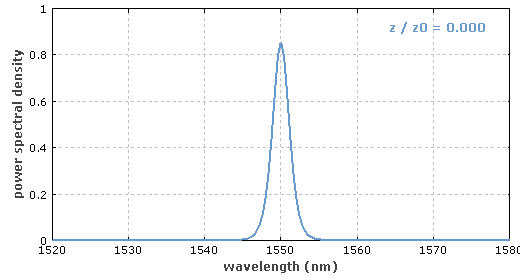
图 1 三阶孤子的时间演化(注:原图为动态图)。
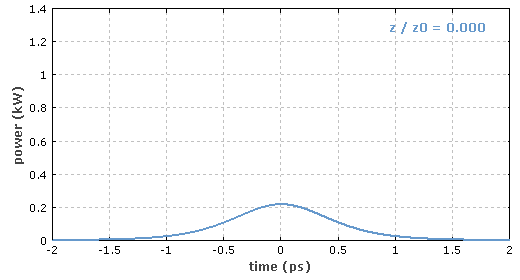
图 2 三阶孤子的光谱演化(注:原图为动态图)。
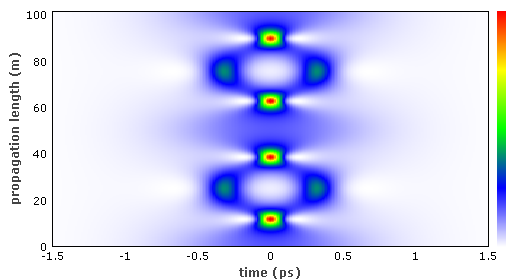
图 3 三阶孤子的时间演化。彩色温标代表光功率。孤子周期为50.4 m,即显示的范围约为两个孤子周期。
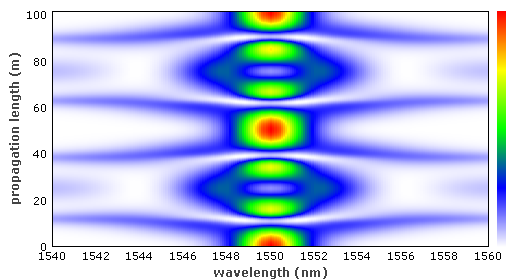
图 4 三阶孤子的光谱演化。彩色温标代表功率谱密度。
高阶孤子可以用于非线性脉冲压缩:具有合适能量的sech2形状的脉冲注入到具有反常色散的光纤中,演化过程为高阶孤子演化,传播一定距离后,脉冲长度显著较小。较高的孤子阶数可以实现很强的压缩,还对泵浦波长有严格的选择。
基本孤子通常比较稳定,而高阶孤子会由于受到各种效应(例如高阶色散,拉曼散射,双光子吸收)的影响分裂成基本孤子。孤子分裂在有些过程中发挥主要的作用,例如,光子晶体光纤中的超连续谱产生。
参考文献
[1] V. E. Zakharov and A. B. Shabat, “Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media”, Sov. Phys. JETP 34, 62 (1972)
[2] L. F. Mollenauer, R. H. Stolen, and J. P. Gordon, “Experimental observation of picosecond pulse narrowing and solitons in optical fibers”, Phys. Rev. Lett. 45 (13), 1095 (1980)
[3] W. Hodel and H. P. Weber, “Decay of femtosecond higher-order solitons in an optical fiber induced by Raman self-pumping”, Opt. Lett. 12 (11), 924 (1987)
[4] S. R. Friberg and K. W. DeLong, “Breakup of bound higher-order solitons”, Opt. Lett. 17 (14), 979 (1992)
参阅:孤子、孤子周期



