定义
Rayleigh-Plesset方程（RP方程）是表征超声作用下单个超声微泡振动的半径随时间变化关系的流体力学方程。
假设
对于Rayleigh-Plesset方程所探讨的单个微泡振动，假设了介质为牛顿流体、均质不可压、微泡周边没有组织和其他微泡的影响；且对于单个微泡，假设微泡是球型的，且振动时仅仅存在径向振动，即振动的结果是R(t)，即微泡半径随时间的改变。
形式
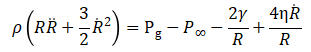
其中，ρ为微泡周边的介质密度，R(t)为微泡的半径，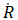
和
分别为微泡半径随时间的一阶导数和二阶导数，Pg为微泡内气压，P∞为微泡外压强，γ为微泡的表面张力，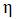
为介质粘度。等式左侧为微泡动量的改变，等式右侧分别为微泡内气压、外界压力、表面张力以及粘性力。
历史地位和后续发展
Rayleigh-Plesset方程是微泡振动的理想化模型，后续所有的微泡振动的方程都是基于Rayleigh-Plesset方程提出的。微泡膜的存在会使微泡更硬，带来谐振频率的上升和非线性效应的下降，微泡膜的存在同时会使微泡更黏，从而导致微泡振动的阻尼更大。微泡处于血液等粘弹性性质同样会改变微泡振动的粘度以及频率，现在的研究思路为套用RP方程，将粘弹性流体的本构关系运用在微泡振动周围介质上。在几何限制中的微泡振动的理论发展方向为结合RP方程，推导在几何限制中的微泡变形；在多微泡的相互作用中，研究者基于RP方程，通过流体力学理论中的气泡间的相互作用力，得到微泡群作用效果。总而言之，弱假设下的微泡振动理论的基本思想为在RP方程中做改进，使微泡的振动理论研究更接近实际。
参阅：超声造影剂、谐波成像
