定义
在高输入功率时放大器增益变小的现象。
放大器装置,例如激光增益介质不可能在任意高的输入功率状态下都保持在一个稳定的增益值,因为这需要将任意的功率加到放大的信号中。因此,增益在高输入功率时会降低,这一现象被称为增益饱和(或者增益压缩)。
在激光增益介质中,增益不会根据输入功率而立刻达到某一值,因为增益介质中储存了一部分能量,而储存的这部分能量决定了增益。例如,突然增加输入到激光增益介质中的功率会在一定时间段内降低增益,因为激光离子激发态数目以一定的速率在减小。这在激光动力学中具有很重要的结果。
增益的基本动力学方程为:
![]()
这里g是增益系数(假设比较小), gss 是小信号增益(给定泵浦能量),τg 是增益弛豫时间,P是放大光束的功率,Esat 是增益介质的饱和能。记住功率放大因子是exp(g),而不是g.
稳态下的增益饱和
在稳态时(也就是长时间内具有稳定的泵浦功率和共振损耗),增益为:
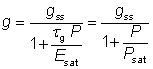
这里Psat 是饱和功率。这里暗含的假设为泵浦速率是一个定值,也就是不存在泵浦饱和效应。这一假设使用于大多数情形,但不是全部。
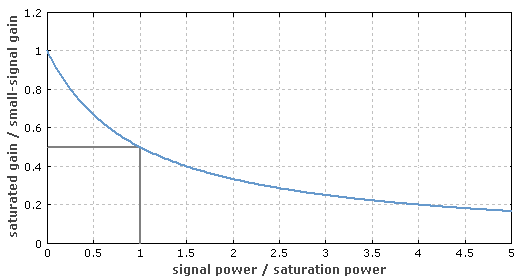
图 1 稳态饱和增益与信号功率的关系(泵浦功率为常数)。
例如,当信号光功率与饱和功率相等时,增益减小到小信号增益的一半。
计算大增益的情况更加复杂,主要是因为放大器中的光强变化很大。直接的方法是将高增益放大器分成一系列小增益的放大器,因此可以采用小增益近似。但是,存在许多更加高效的数值模拟技术,不需要这种拆分过程。
激光束光强横向的变化会改变饱和特性:在激光束外侧的激光活性离子需要更高的光功率才能达到饱和。这一效应也改变了饱和曲线,如图(1)和(2)所示。
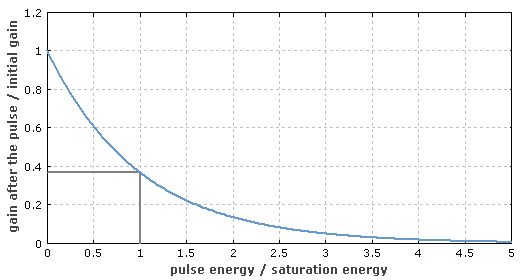
图 2 采用短脉冲增益的减小。
上面给出的方程也可以用于低脉冲能量高重复率的脉冲列中。这时饱和增益只由平均功率决定。
光脉冲的增益饱和
当放大短脉冲时(持续时间小于上能级寿命),在脉冲放大过程中的自发辐射不重要。另外,泵浦光的影响也可以忽略(高泵浦脉冲强度的情况除外)。脉冲过后的增益减小倍数为exp(−Ep / Esat),这里Ep 为泵浦能。例如,当Ep = Esat时,增益减小到初始值的1/e约37%。
脉冲经历的有效增益是一个平均值,在脉冲放大过程中增益会减小。这一平均增益可以通过考虑增益介质中储存能量的减小来进行计算。在更简单的情况,增益很小时,放大器中的光强几乎为常熟,那么结果变为:
![]()
这里g0 是初始增益系数。更一般的情况是对于任意高的增益,可以采用Frantz-Nodvick方程:
![]()
然后得到:
![]()
注意暗含的近似就是涉及到的能级系统总是存在热平衡态。在强飞秒脉冲的情况下这种近似就不适用了。在这种情况下,有效放大过程和能量提取会比之前方程推测的要少。
均匀和非均匀饱和
一个非常重要的问题是增益饱和的均匀或者非均匀性。均匀增益饱和表示增益谱的形状不会受饱和效应的影响。当所有激光活性离子具有相同的辐射谱时就是这种情况。在有些增益介质中,尤其是无序性介质例如玻璃,激光活性离子可能占据晶格中不同的态,不同的局域电场会影响跃迁波长和强度。这回导致非均匀饱和(图3),这里增益谱形状改变;通常来讲,激光波长附近的增益比其它波长处更容易发生饱和效应。
 图 3 非均匀增益饱和示意图。1064nm的激光饱和增益在1064nm处的程度比其它波长的增益更高。非饱和增益(无激光功率)的情况为虚线作为对比。
图 3 非均匀增益饱和示意图。1064nm的激光饱和增益在1064nm处的程度比其它波长的增益更高。非饱和增益(无激光功率)的情况为虚线作为对比。
另外一个引起非均匀增益的因素为线型激光振荡器中的空间烧孔效应,由增益介质中随波长变化的驻波形式引起。
无论何种情况下的非均匀增益饱和都会使单频工作很难实现,因为增益更倾向于发生在非激光谐振模式。饱和增益的均匀和非均匀性对锁模行为很重要影响,特别是调Q开关和放大器中。
不同增益介质的饱和特性
不同的增益介质在增益饱和性质上差别很大:
1、基于掺杂离子的晶体或玻璃的固态增益介质通常工作在被抑制的跃迁处,因此具有很小的激光截面,很大的饱和影响和强度,长上能级寿命(微秒或毫秒)。这些激光器适宜于调Q开关,但通常有闪烁行为倾向。对于无源锁模情况,通常具有调Q开关不稳定性。
2、半导体和激光染料通常具有比较小的饱和效应和强度,同时上能级寿命很短,通常为几个纳秒。因此不适用于调Q开关,但是对于不存在调Q开关不稳定性的无源锁模,他们对于变化的泵浦功率反应很快。后者对强度噪声由影响。
3、光学参量放大器可以很快将增益调到放大信号的量级,因为在增益介质中不储存能量。
参阅:饱和吸收、激光动力学、非均匀饱和、空间烧孔效应、物理原理



